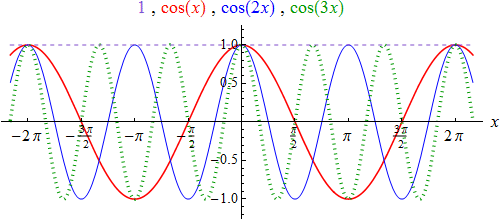
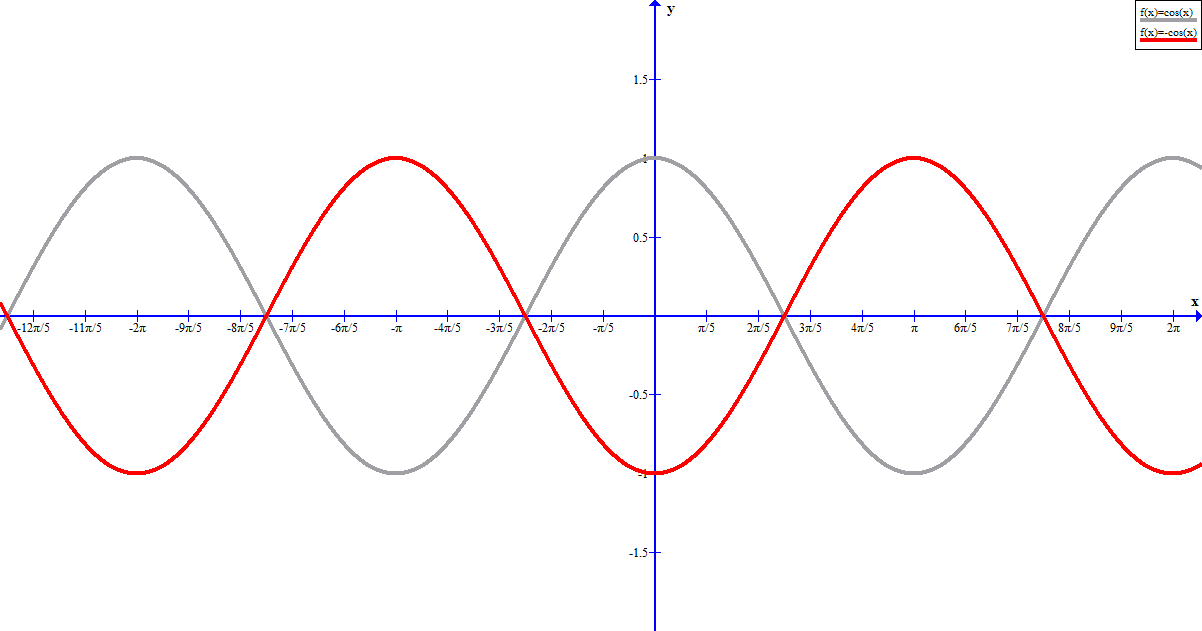
Graph of cos(x) is symmetric about the y axis You get the same values as output for every pair of positive and negative input x Thus, cos(x) is an even function f(x) = cos (x) = cos (x) Check Let x = π/4 f(x) =Cos(π/4) =1/√2 f(x) = Cos(π/4) = 1/√2 = f(x) Here, we need to note that ( π/4) lies in the 4th quadrantCalculus Using the first and second derivative, sketch the graph of f(x) = sin(x) cos(x)Graph the function y = cos(x) 7 and explain how to find the number of times the gum returns to the wall as it travels a distance of 60 feet The gum returns to the wall each time the graph shows a minimum value of 6 (the height of the wall) Count the number of minimums that occur between x = 0 ft and x = 60 (but omit the first time when x = 0)

Plot Of The Function I X F X 1 Cos X Cosh Rx For Values Of R Download Scientific Diagram
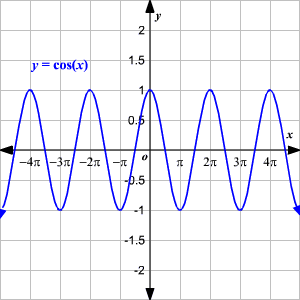
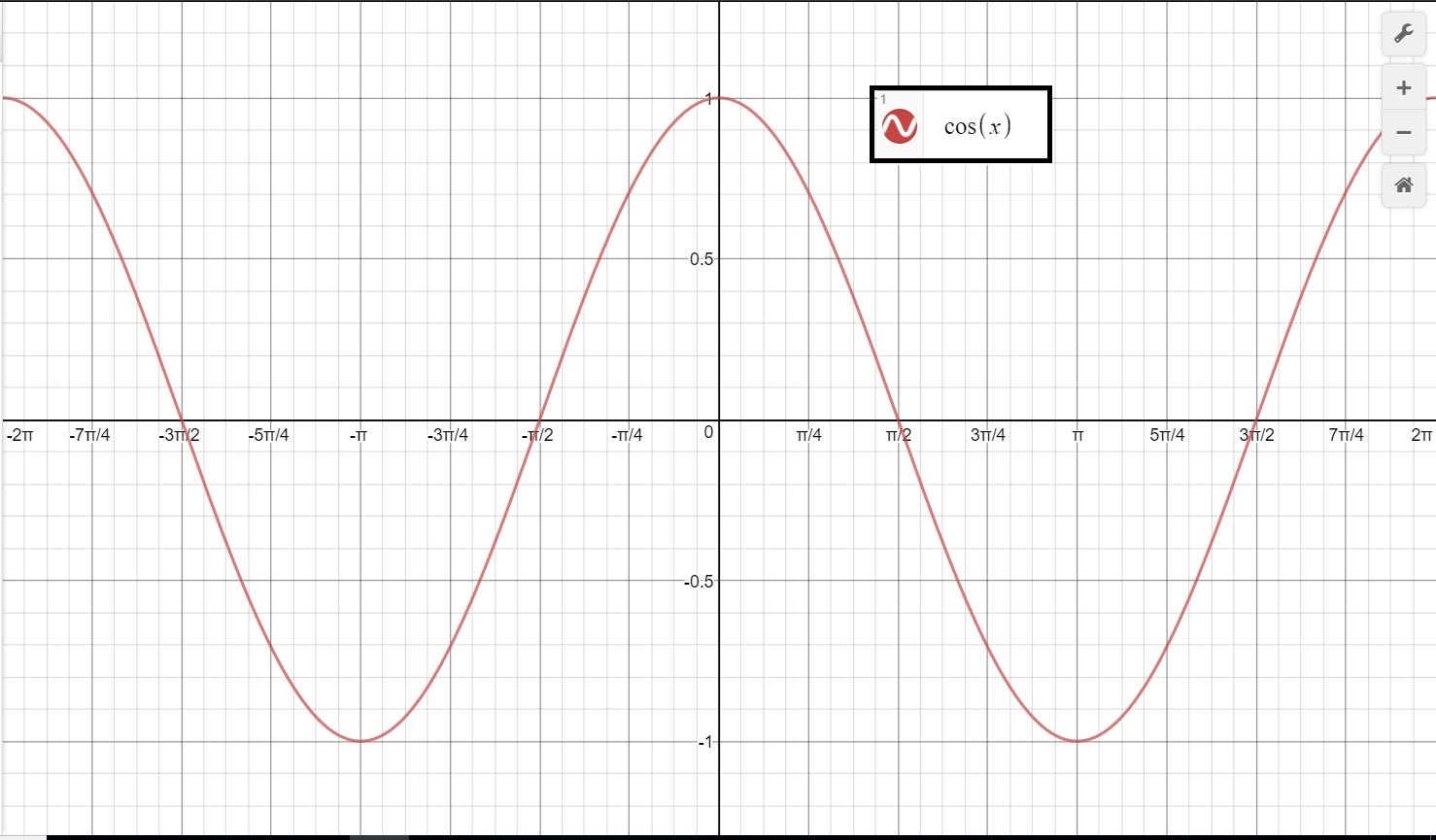
F(x)=cos x graph
F(x)=cos x graph-Y y axis f (x)=f (x) f (−x) = −f (x) In other words, the graph is symmetric about origin f (0)=f (0)\implies f (0)=0 f (−0) = −f (0) f (0) = 0 That is, an odd function must pass through the origin From this definition, the cosine function is an even function and the sine function is an odd function f (x) = cosx ⇒ f '(x) = −sinx This is the graph of y = f (x) And this is a graph of its derivative y = f '(x)



Graphs Of The Sine And Cosine Function Precalculus Ii
New Blank Graph Examples Lines Slope Intercept Form example Lines Point Slope Form example Lines TwoDerivative of f (x) = arccos (cos (x)) and its Graph f (x) is a composite function and the derivative is computed using the chain rule as follows Let u = cos (x) Hence f (x) = arccos (u (x)) Apply the chain rule of differentiationI'm trying to draw in tikz the graph of f(x)=x*cos(1/x) and I'm using the following code \documentclass10pt{article} \usepackage{pgf,tikz} \usetikzlibrary{arrows
Graphing Sine & Cosine Functions (II) Author Tim Brzezinski Topic Cosine, Functions, Function Graph, Sine, Trigonometric Functions Interact with the applet below for a few minutes Then answer the questions that follow Questions 1) Consider the function f (x) = sin (x) What are the values of a, b, c, and d for this parent sine function?Trigonometry Graph f (x)=cos (x) f (x) = cos (x) f ( x) = cos ( x) Use the form acos(bx−c) d a cos ( b x c) d to find the variables used to find the amplitude, period, phase shift, and vertical shift a = 1 a = 1 b = 1 b = 1 c = 0 c = 0 d = 0 d = 0 Find the amplitude a a Below are the graphs of the three trigonometry functions sin x, cos x, and tan x In these trigonometry graphs, xaxis values of the angles are in radians, and on the yaxis, its f(x) is taken, the value of the function at each given angle Sin Graph y = sin x;
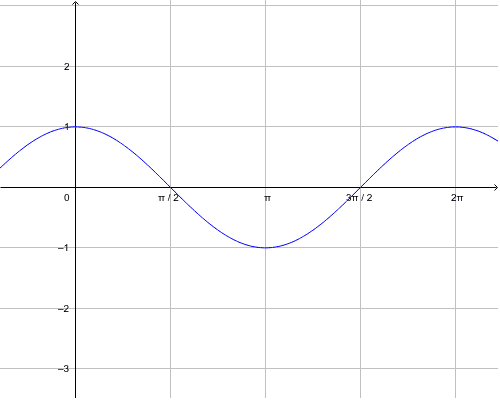
To graph f (x) = 1 cos(x), start working on it's Parent Function f (x) = cos(x) first Make a table of values for f (x) = cos(x) and f (x) = 1 cos(x) For x, consider the values 0, π 2,π, 3π 2 and 2π If you examine Col 4 and Col 5, you see that the difference is 1 Graph of y = f (x) = cosThe roots or zeros of y = sin x is at the multiples of π; I was wrong when I wrote cos x (which is a function pair, so the graph of cos x is no problem) Actually, I wanted to do was make the graph of f (x) = sin x , and I thought I'd just ask a simple question (f(x) = sinx )and, after suggestions, I would complete the rest



Solution Graph Each Sinusoidal Function Over Two Complete Cycles A F X 2 Cos X 3 B F X 4 Sin X 2 C F X 1 2 Cos X 3 Can You Please Help Me Thank You




Help Please What Trigonometric Function Represents The Graph F X 4 Sin X Pi Over 2 F X Brainly Com
Mac, we have two responses for you Hi Mac, I would be guided by the graphs of the sine and cosine near x = 0 For the cosine function, when x is close to zero (actually between π /2 and π /2), cos(x) = cos(x) and hence near x = 0 cos(x) = cos(x) and thus lim h>0 (cosh cos0)/(h) = lim h>0 (cos(h) cos0)/(h) = 0 (not 1 as you said in your question)The graph of the function f(x) = 3 sin x 4 cos x is a sine wave that has been translated Calculate by how many degrees and in which direction the wave has been translated f(x) = 3 sin x 4 cos x = 5 sin (x v) v = tan −1 (4 / 3) ≈ 531° The wave has been translated by 531° to the left (f(x) ≈ 5 sin (x 531°) Example 3 The graph of y=sin(x) is like a wave that forever oscillates between 1 and 1, in a shape that repeats itself every 2π units Specifically, this means that the domain of sin(x) is all real numbers, and the range is 1,1 See how we find the graph of y=sin(x) using the unitcircle definition of sin(x)



Use The Graph Of The Function To Answer The Following Wyzant Ask An Expert



How Do You Graph The Derivative Of F X Cos X Socratic
Trigonometry Graph f (x)=cos (x/2) f (x) = cos ( x 2) f ( x) = cos ( x 2) Use the form acos(bx−c) d a cos ( b x c) d to find the variables used to find the amplitude, period, phase shift, and vertical shift a = 1 a = 1 b = 1 2 b = 1 2 c = 0 c = 0 d = 0 d = 0 Find the amplitude a aGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Section 71 Transformations of Graphs In Chapter 4 we saw that the amplitude, period, and midline of a sinusoidal graph are determined by the coefficients in its formula The circular functions (sine and cosine of real numbers) behave the same way Subsection Period, Midline, and Amplitude Changes to the amplitude, period, and midline are called transformations of the basic sine and cosine



Math Scene Trigonometry Rules Lesson 3



Which Quadrants And Axes Does F X Cosx Pass Through Socratic
The graph of f(x) = Sin x Cos x is as shown below For further understanding, you can refer to the video PS Variable x is in terms of radians here Edit 1 Thanks for pointing out Adithya Shashidhara that may mean the least integGraph f(x) = cos(x) Trigonometric Functions A trigonometric function is a function which is used to find the relationship between the sides of a triangle Trigonometry functions can be graphedQuestion Find the first three xintercepts of the graph of the given function on the positive xaxis f(x) = 9 18 cos(xπ/3) Found 2 solutions by lwsshak3, Edwin McCravy




Use The Graph Below To Answer The Question That Follows What Trigonometric Function Represents The Brainly Com



Ich Soll Den Graph Der Funktion F X Sin X Cos X Erstellen Habe Aber Null Peilung Wer Kann Helfen Mathelounge
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreProblem 29 Easy Difficulty (a) By graphing the function f ( x) = ( cos 2 x − cos x) / x 2 and zooming in toward the point where the graph crosses the y axis , estimate the value of lim x → 0 f ( x) (b) Check your answer in part (a) by evaluating f ( x) for values of x that approach 0 Sketch the graph Sketch a graph of \(h(x)=5\dfrac{1}{2}\sec 4x\) over the interval \(0,2\pi \) If you compare this example to \(f(x)=\sec x\), it will be translated 5 units up, with an amplitude of \(\dfrac{1}{2}\) and a frequency of 4 This means in our interval of 0 to \(2\pi \), there will be 4 secant curves



In The Diagram The Graphs Of F X Cos X And G X Sin X B Are Drawn For The Interval 180 Circ Leq X Leq 90 Circ Mathsgee Answer Hub



2
Question Graph f(x) = 3 cos x and g(x) = cos x1 in the same rectangular coordinate system for 0 sxs 2n Then solve a trigonometric equation to determine points of intersection and identify these points on the graph The graphs of f(x) and g(x) are plotted together The graph of f(x) is the solid line and the graph of g(x) is the dashed lineWe can define an inverse function, denoted f(x) = sin−1 x or f(x) = arcsinx, by restricting the domain of the sine function 3 The cosine function f(x) = cosx We shall now look at the cosine function, f(x) = cosx This function can be defined for any number x using a diagram like this x cos x 1 wwwmathcentreacuk 5 c mathcentre 09 The graph of f is concave downward on the interval (negative infinity, 0) C The graph of f is concave trig Graph three periods of the function (identify period and phase shift and intercepts) y = f(x) = √3/2 sin(2x) 1/2 cos(2x) if you can't graph it can you at least get it into that simpler form which is graph able college algebra



Betrachtungen Zur Periode




Graph Of Cosine Function Mathtestpreparation Com
Over $0,2 \pi$, we have $$ f(x) = \cos(x) \sin(x) = \begin{cases} \cos(x) \sin(x) & 0 \leq x < \pi/2\\ \cos(x) \sin(x) & \pi/2 \leq x Draw individual graphs in individual domains and you should get the desired graph Also, it looks linear just because of the scale you have chosen Actually, it is as sinusoidal as sine is in theRelationship between Sine and Cosine graphs The graph of sine has the same shape as the graph of cosine Indeed, the graph of sine can be obtained by translating the graph of cosine by ( 4 n 1) π 2 \frac { (4n1)\pi} {2} 2(4n1)π units along the positiveAbout Beyond simple math and grouping (like "(x2)(x4)"), there are some functions you can use as well Look below to see them all They are mostly standard functions written as you might expect




Trig Transformations Of Graphs



Graph Sine And Cosine Functions
(a) By graphing the function f(x) = (cos 2x − cos x)/x2 and zooming in toward the point where the graph crosses the yaxis, estimate the value of lim x → 0 f(x) (b) Check your answer in part (a) by evaluating f(x) for values Algebra 2 Which cosine function has maximum of 4, a minimum of 4, and a period of 2pi/3?F(x)=cosx f(x)=cosx Log InorSign Up f x = cosx 1 2 functions $$ ($$) $$ < $$ > $$ 4 $$ 5 $$ 6 $$ × $$ a $$, $$ ≤ $$ ≥ $$ 1 $$ 2 $$ 3 $$ − A B C $$ $$ π $$ 0 $$ $$ = $$ Sign UporLog In to save your graphs!Figure 442 The graph of f (x) = (cos x) / x 1 f (x) = (cos x) / x 1 crosses its horizontal asymptote y = 1 y = 1 an infinite number of times The algebraic limit laws and squeeze theorem we introduced in Introduction to Limits also apply to limits at infinity We illustrate how to use these laws to compute several limits at infinity




Graph Of The Function F X Sin X Cos X 3 In The Interval 0 2p Download Scientific Diagram



How To Plot The Graph Of X Cos X Quora
Use the Sum Formula for Cosine Factor out \cos (x) Rewrite the limit Use the fact that x is a constant when computing limits as h goes to 0 The limit \lim_ {x\to 0}\frac {\sin (x)} {x} is 1 To evaluate the limit \lim_ {h\to 0}\frac {\cos (h)1} {h}, first multiply the numerator and denominator by \cosMake a complete graph of f(x) = x 2 cos(x) \ on \ 2\pi, 2\pi A ferris wheel is meters in diameter and boarded in the six o' clock position, at t = 0, from a platform that is 4 meters aboveThe sin graph passes the xaxis as sin x = 0 there;




3d Plot Of The Function F X Y Z C Cos X Download Scientific Diagram




1 Graphs Of F X X Tan X 1 Solid And G X X Sin X Cos X Download Scientific Diagram
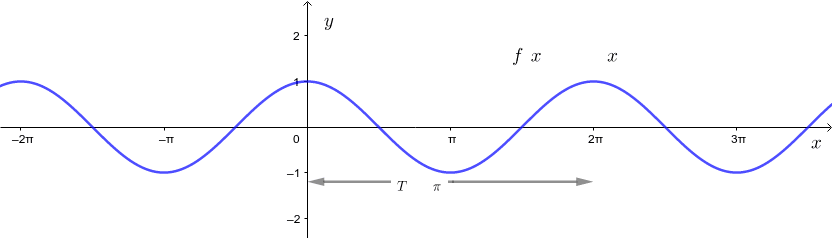
Transcribed image text Consider the function f(x) = 22 COS X The graph of this function is provided below Find the area of the region that is bounded by the graph of f(x) and the xaxis on the interval 2, 2 y y = f(x) 2 → X 2The sine and cosine functions have several distinct characteristics They are periodic functions with a period of 2π The domain of each function is ( − ∞, ∞) and the range is − 1, 1 The graph of y = sin x is symmetric about the origin, because it is an odd functionGraphs of trigonometric functions The graph of the cosine function f ( x) = cos x To draw the graph of the cosine function divide the unit circle and x axis of a Cartesian coordinate system the same way as when drawing the sine function



Cos Graph



Betrachtungen Zur Periode
For – y=f(x)=tan(x) Range All real numbers (or y ∈ R) Tangent's Domain Defined for all x real values, except x ≠(2n 1)(π/2), where n is any integer Period π Tangent is an odd function As a result from the above domain and range, changes will affect range but will affect the domain The Graph of tan(x) functionFor example, the range of f(x) = sin x is the set of all real numbers between −1 and 1 (ie the interval −1,1), whereas the range of f(x) = tan x is the set of all real numbers, as we can see from their graphs A function f(x) is periodic if there exists a number p > 0 such that x p is in the domain of f(x) whenever x is, and if theFor real number x, the notations sin x, cos x, etc refer to the value of the trigonometric functions evaluated at an angle of x rad If units of degrees are intended, the degree sign must be explicitly shown (eg, sin x°, cos x°, etc)



1



How Do You Use The Amplitude And Period To Graph F X 4 Cos X Pi 2 Socratic
The basic sine and cosine functions have a period of 2\pi The function \sin x is odd, so its graph is symmetric about the origin The function \cos x is even, so its graph is symmetric about the y axis The graph of a sinusoidal function has the same general shape as a sine or cosine functionCosine f x x( ) cos= Since the period of the cosine function is 2π, we will graph the function on the interval 0, 2π The rest of the graph is made up of repetitions of this portionFunctions & Graphing Calculator \square!




Graph Of F X Sin X Cos X Youtube
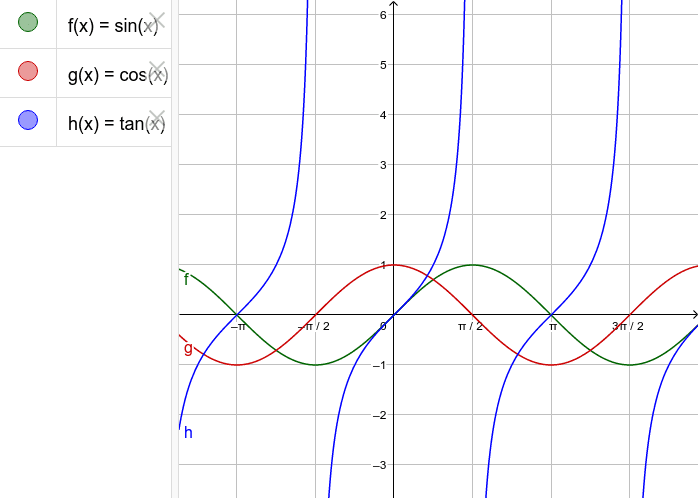



The Functions Sin X Cos X And Tan X Geogebra




Integral Of Cos X Add Just A Bit Of Pi



Graphing The Trigonometric Functions Opencurriculum




Proof Of The Derivative Of Cos X Video Khan Academy



What Is The Range Of The Function Y Cos X Socratic
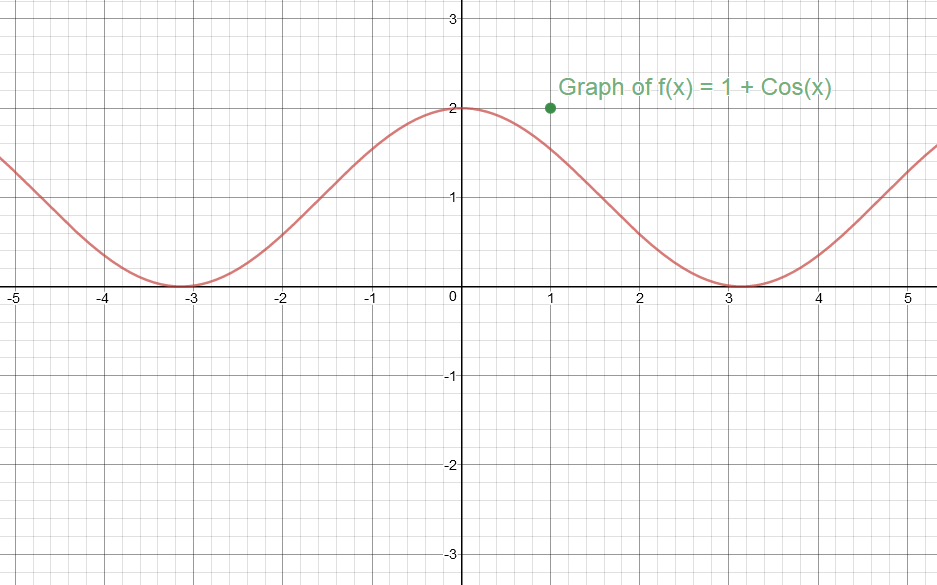



How Do You Graph F X 1 Cosx Socratic




Center Of A Circle Rolling On The Graph Of A Sinusoidal Function Say F X 3 Cos X 3 Mathematics Stack Exchange
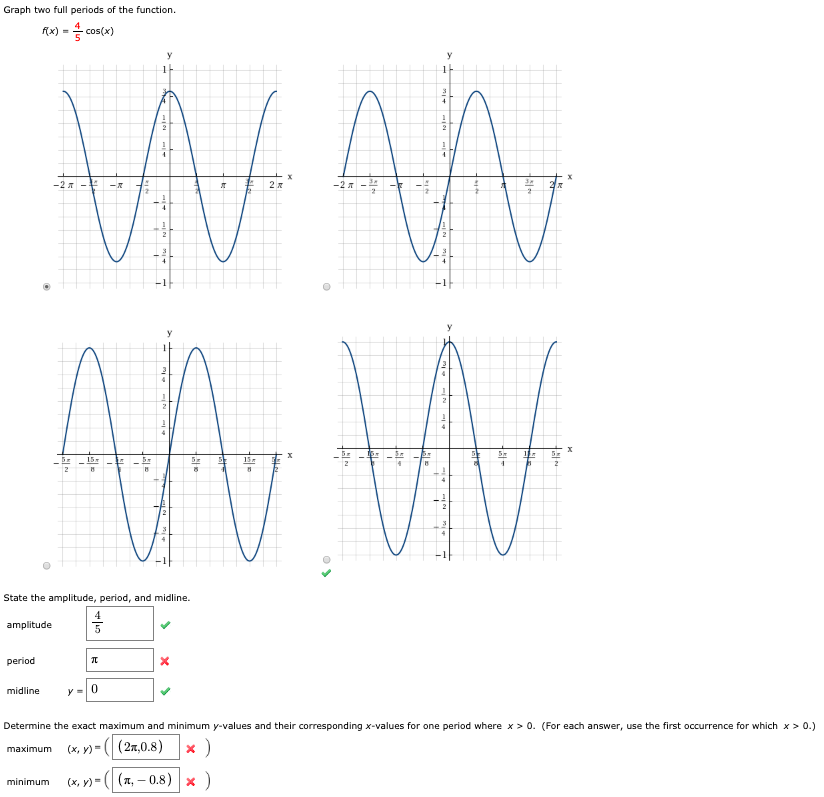



Graph Two Full Periods Of The Function F X Cos X Chegg Com




The Number Of Points Where F X Sin X Cosx Where Denotes The Greatest Integer Fun Youtube




Find A And D For F X A Cos X D Such That The Graph Of F Matches The Figure Study Com



The Graph Of The Cosine Function F X Cos X Properties Of The Cosine Function




Derivatives Of Trig Functions
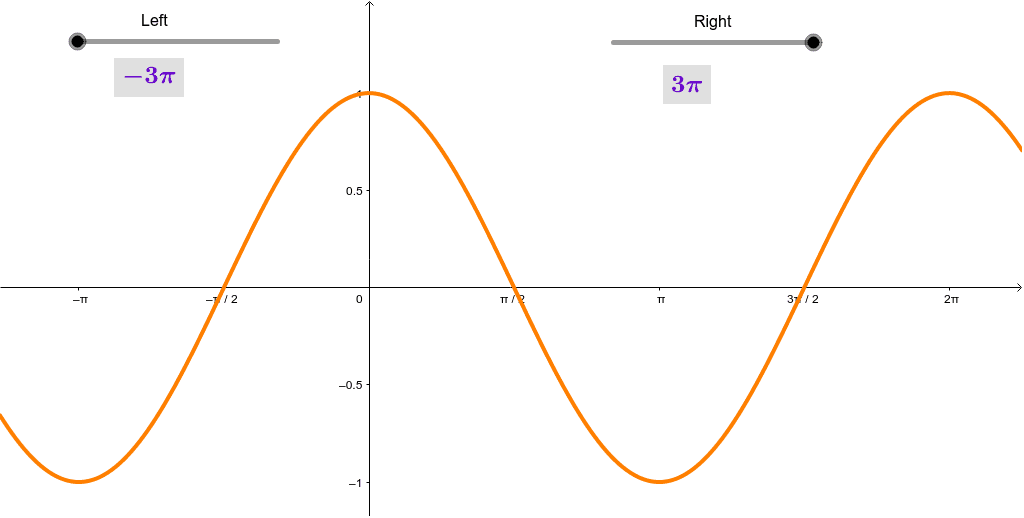



Is Y Cos X One To One Geogebra



1




Usage A Graphing Utility To Graph The Function F X Chegg Com



Graphs Of The Sine And Cosine Function Precalculus Ii




Graph Of F X Sin X 1 Cos X Youtube




How To Find The Inverse If F X X Cos X Then Find F X Quora
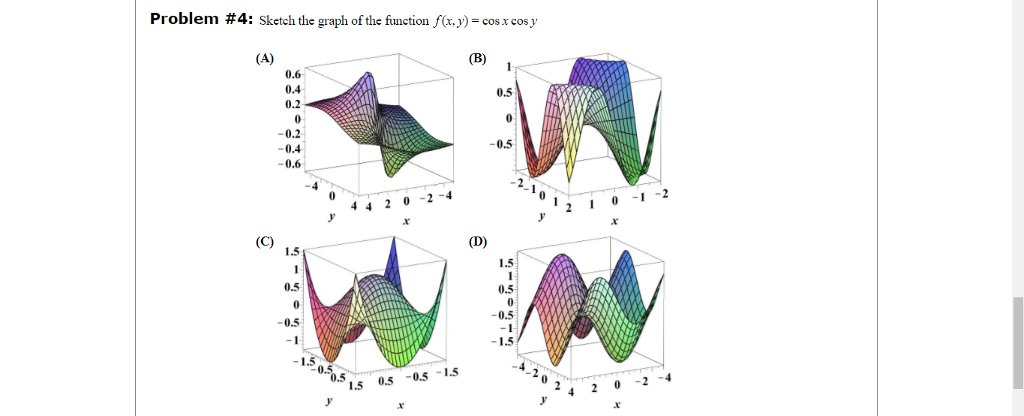



Problem 4 Sketch The Graph Ofthe Function Chegg Com




The Graph Of Cosine Y Cos X Youtube
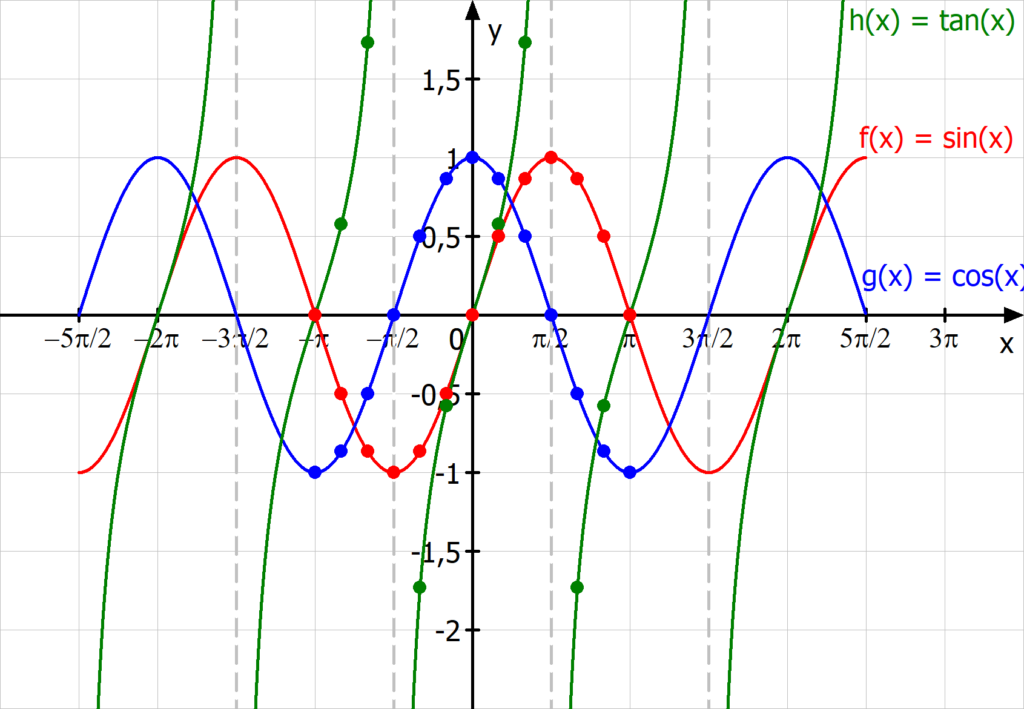



Trigonometrische Funktionen Definition Und Beispiele Mit Video



Grafica Funcion F X Cos X Geogebra



F X Cos X Geogebra



How Do You Graph Y 3 Cosx Socratic



Ich Soll Den Graph Der Funktion F X Sin X Cos X Erstellen Habe Aber Null Peilung Wer Kann Helfen Mathelounge



Solution Sketch The Graph Of The Function Show Your Solution 1 F X 1 4 Sin X 2 F X 4 Cos X Please Do Help Me Thanks
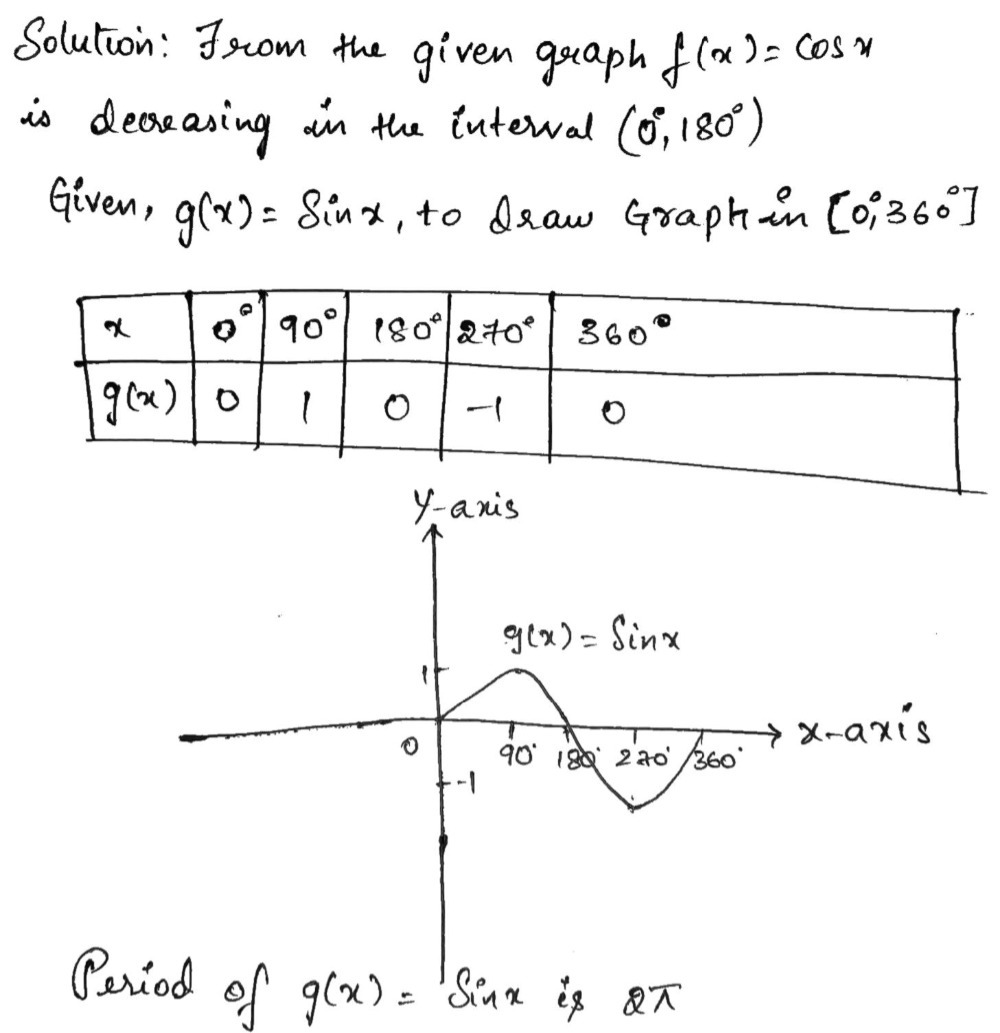



In The Diagram Below The Graph Of Fx Cos X Is Dra Gauthmath



Graph Of The Function Y Cos X



Answered On The Graph Of F X Cos X And The Bartleby



Trigonometric Functions
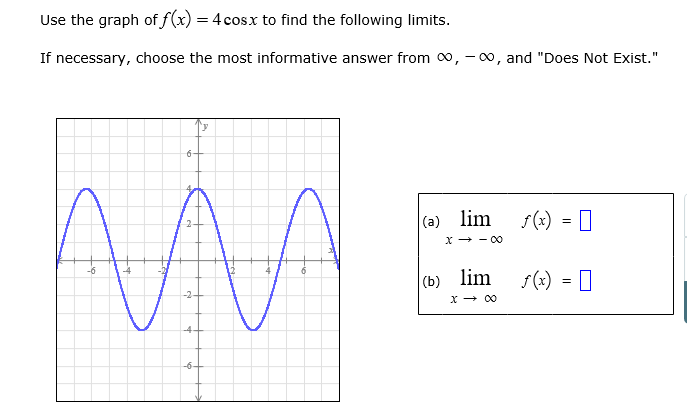



Use The Graph Of F X 4 Cos X To Find The Following Chegg Com
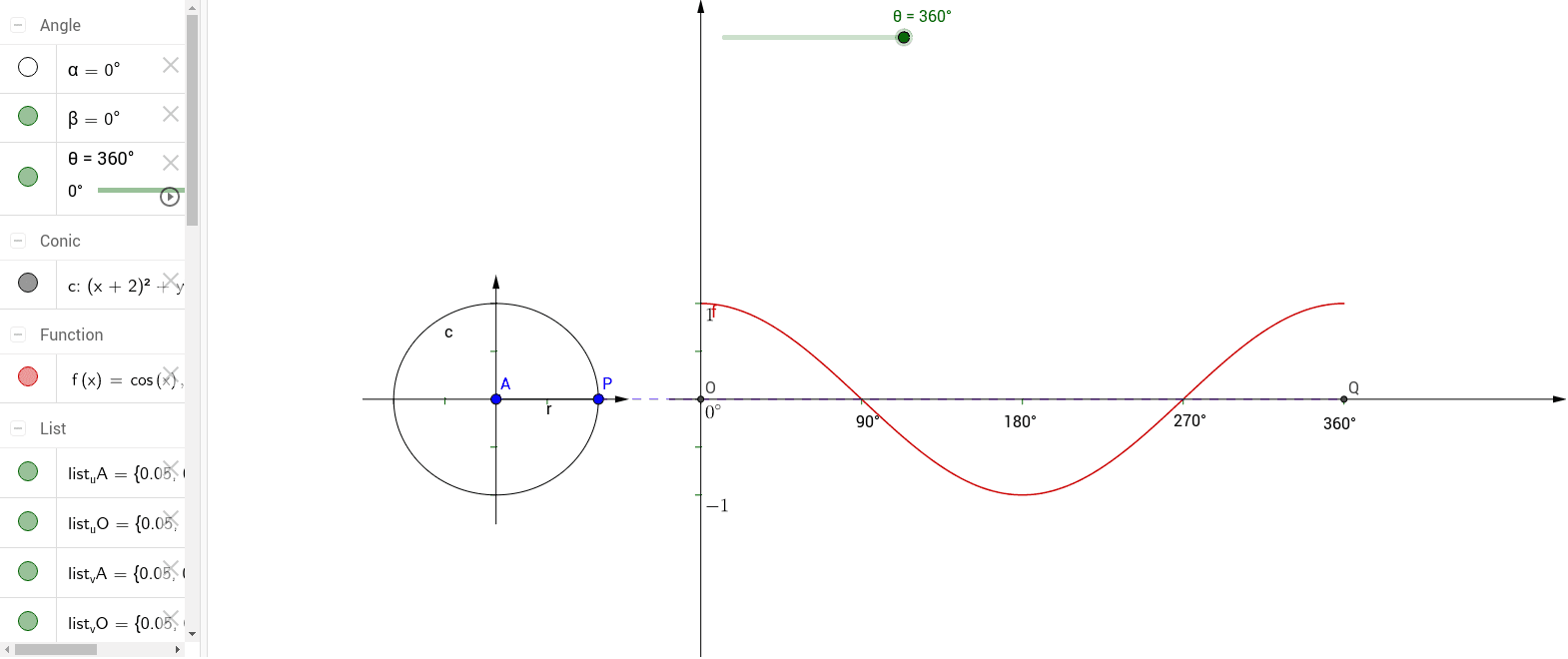



Trigonometric Functions Graph Cos X Geogebra



Sketch The Graphs Of The Following Trigonometric Functions I F X Cos X P 4 Ii G X Cos X P 4 Iii H X Cos 2 2x Sarthaks Econnect Largest Online Education Community




Find The No Of Points Of Non Differentiability Of F X Max Sinx Cosx 0 In X Epsilon 0 2 Pi




How To Find The Period Of Cosine Functions Video Lesson Transcript Study Com
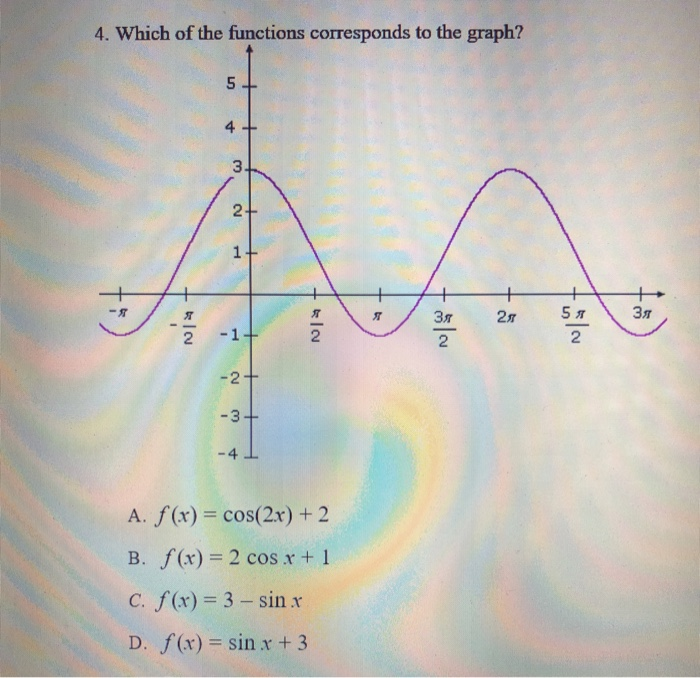



4 Which Of The Functions Corresponds To The Graph 2 Chegg Com



The Graph Of The Cosine Function F X Cos X Properties Of The Cosine Function




Ableitung Cosinus Erklarung Beispiele Mit Video



Find Derivative Of F X Arccos Cos X And Graph It



How Do You Graph F X 1 Cosx Socratic




4 5 Graphs Of Sine And Cosine A Function Is Periodic If F X Np F X For Every X In The Domain Of F Every Integer N And Some Positive Number



3




Sketch The Graph Of The Following Trigonometric Functions F X Cos X P 4 Mathematics Shaalaa Com




Ixl Write Equations Of Cosine Functions From Graphs Algebra 2 Practice



Draw The Graph Of Y Cos X X In 0 2pi Where Rep



3



Plotting F X Sin X And F X Cos X On Pgf Tikz Tex Latex Stack Exchange




Answered Let Cos X If X 0 F X If X 0 1 Bartleby




Plot Of The Function I X F X 1 Cos X Cosh Rx For Values Of R Download Scientific Diagram




How To Graph Cos X Video Lesson Transcript Study Com



Fourier Series
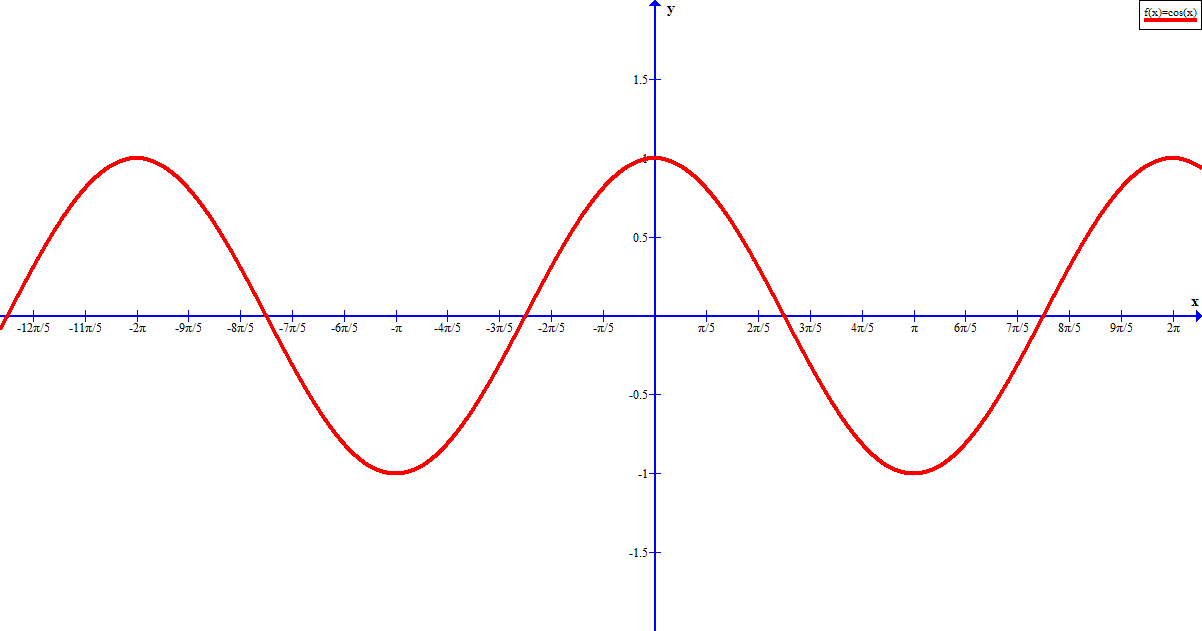



How Do You Graph Y 3 Cosx Socratic




Amplitude Period And Frequency Ck 12 Foundation



In The Diagram Below The Graph Of Fx Cos X Is Dra Gauthmath



Find A And D For The Function F X A Cos X D Such That The Graph Of F Matches The Figure Wyzant Ask An Expert



F X Cos X G X Cos 2x Describe The Relationship Between The Graphs Of F And G Consider Amplitude Period And Shifts Enotes Com




How To Graph Cos X Video Lesson Transcript Study Com



How Do You Graph Y Cosx 3 Socratic



Explorations With Sine And Cosine




How Do You Graph F X Sinx Sqrt 3 Cos X For X Is Between 0 2pi Homeworklib



Graphing The Trigonometric Functions Opencurriculum



Derfunc



Graphs Of Sin X Cos X And Tan X Gcse Maths Marked By Teachers Com
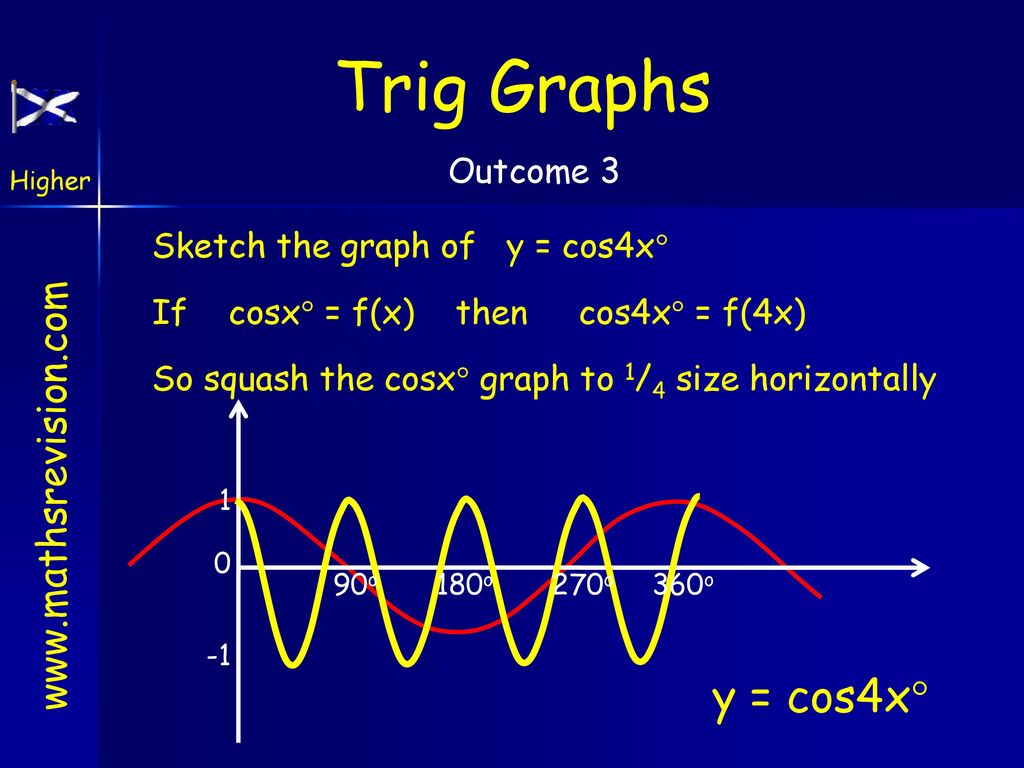



Graph Transformations Ppt Download



Fourier Series
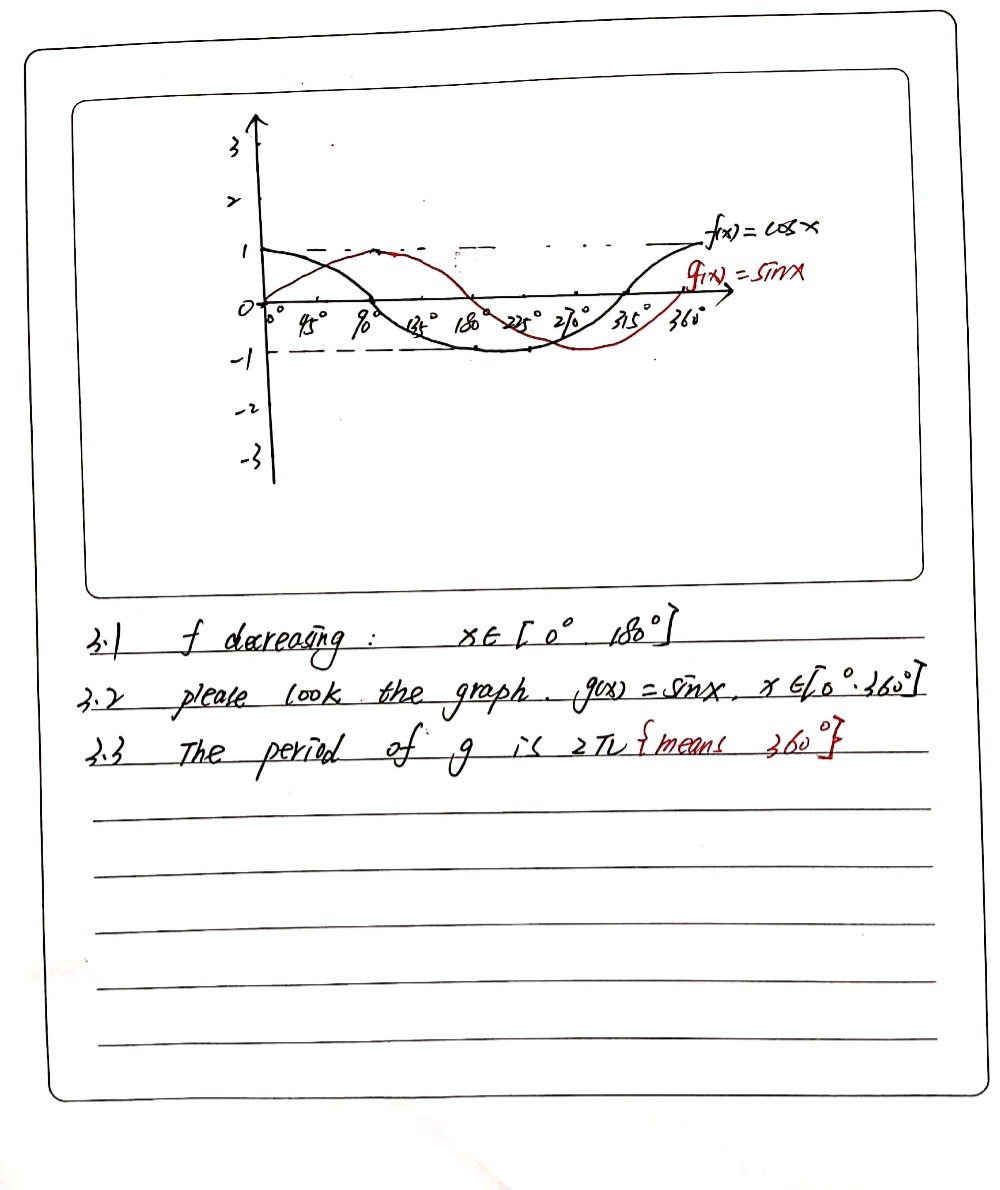



In The Diagram Below The Graph Of Fx Cos X Is Dra Gauthmath



Math Scene Trigonometry Functions Graphs Of Trig Functions Lesson 3



Solution Compare The Graph Of F X Cos 3x With The Graph Of Y Cos X Comparing These Two Graphs Shows That The Period Of F X Is



Problems For Week 1 Additional Exercises 1 If F X X Cos X Find
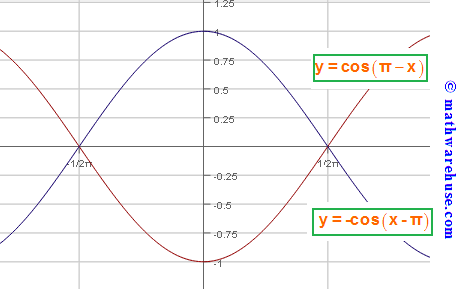



Translation And Phase Shifts Of Sine And Cosine Graphs How Equation Relates To Graph Illustrated Demonstrations And Examples



Find Derivative Of F X Arccos Cos X And Graph It




Which Function Describes The Graph Below F X 6 Cos X F X 3 Cos X 3 F X 6 Sin X F X Brainly Com
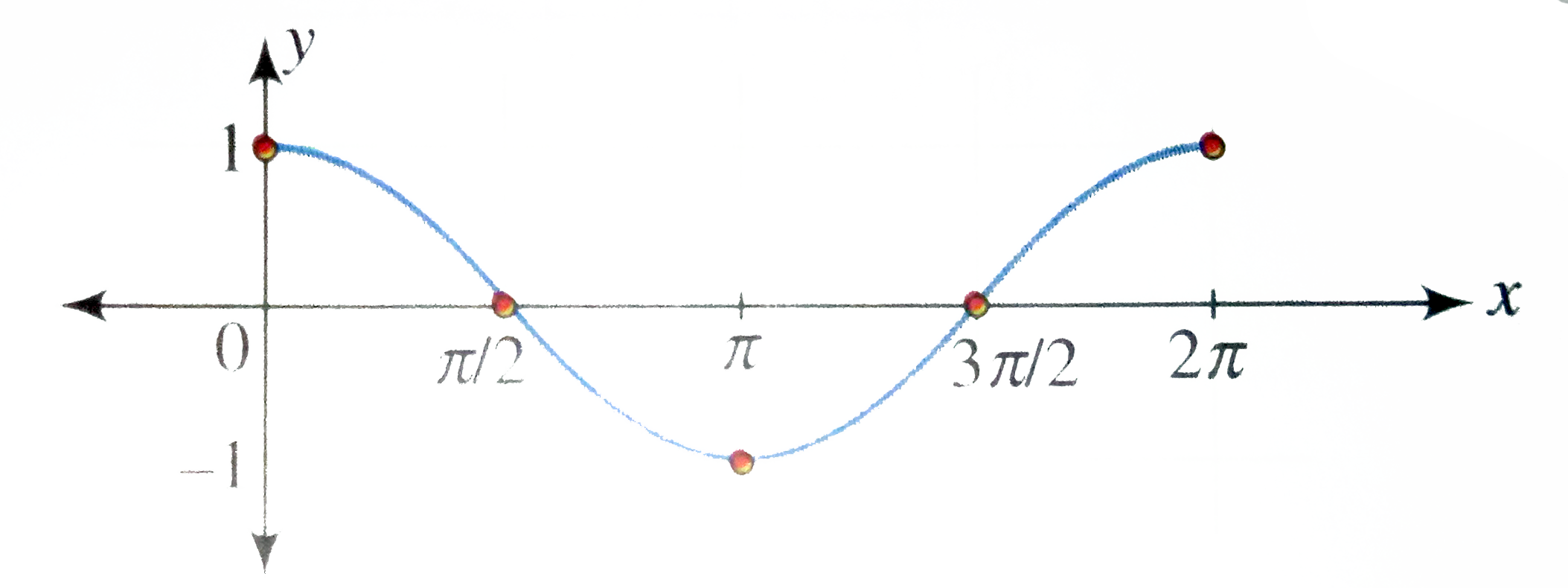



Draw The Graph Of Y Cos X X In 0 2pi Where Represents The Greatest Integer Function
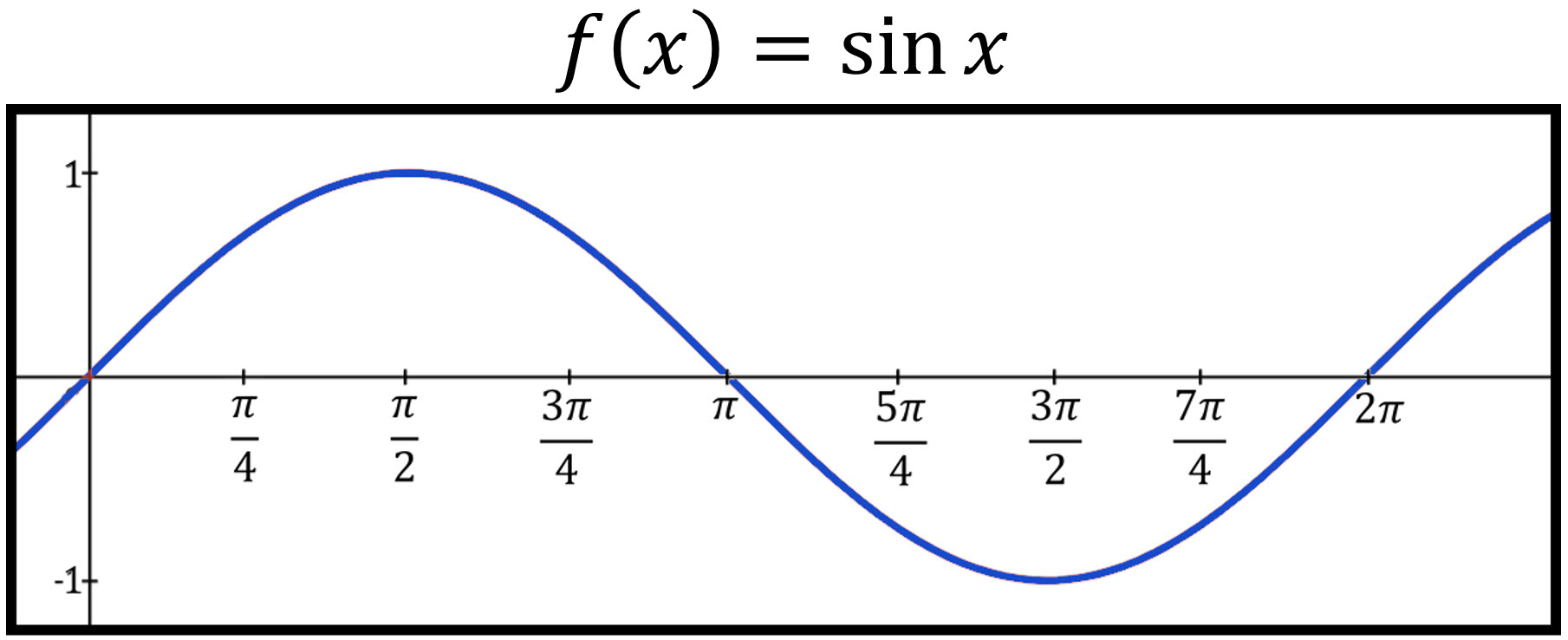



Graphing Trig Functions Sin And Cos Andymath Com
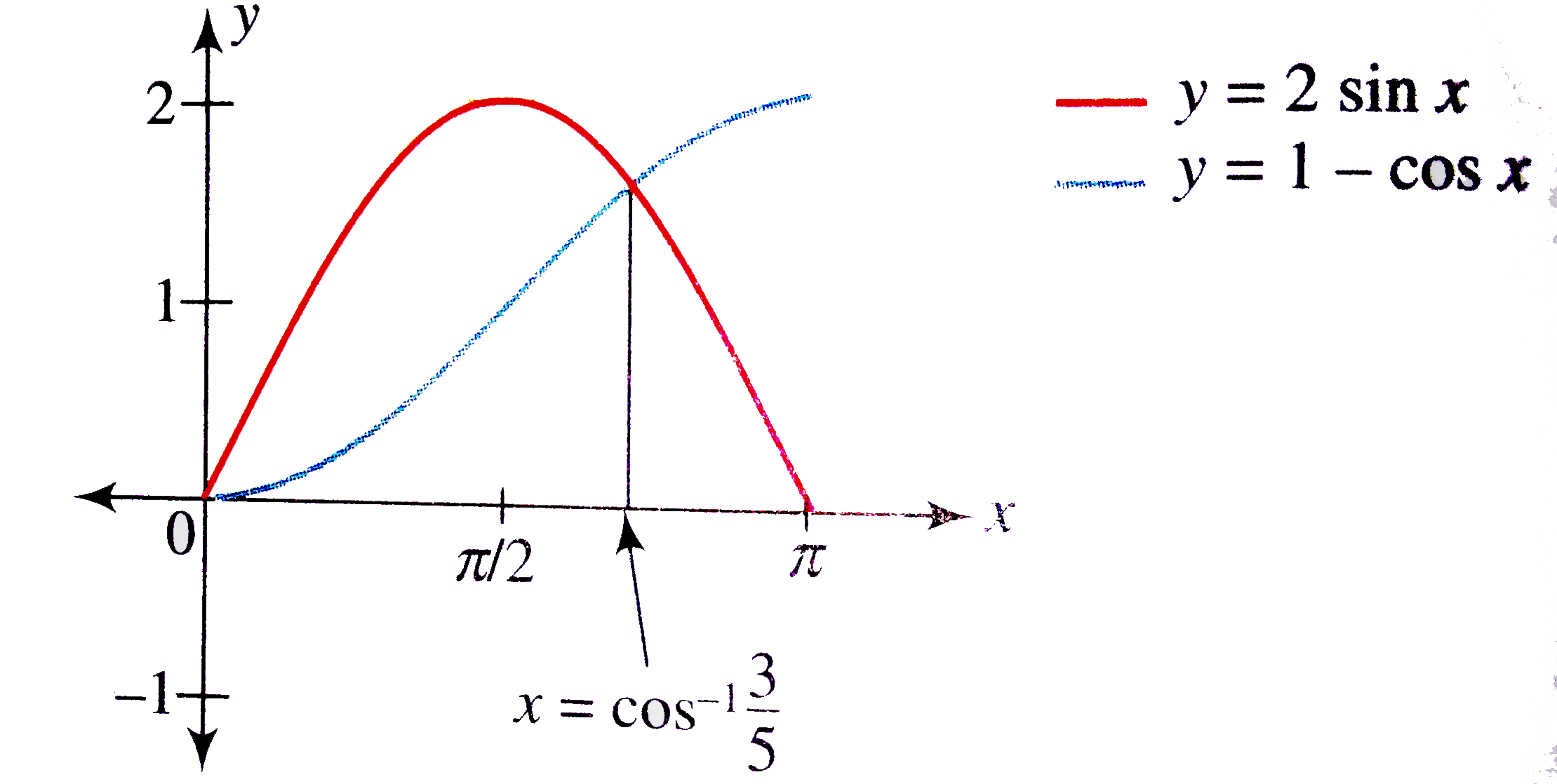



Draw The Graph Of F X Maximum 2 Sin X 1 Cos X X In 0 Pi Also Find The Range Of G X Min 2 Sin X 1 Cos X X In 0 Pi
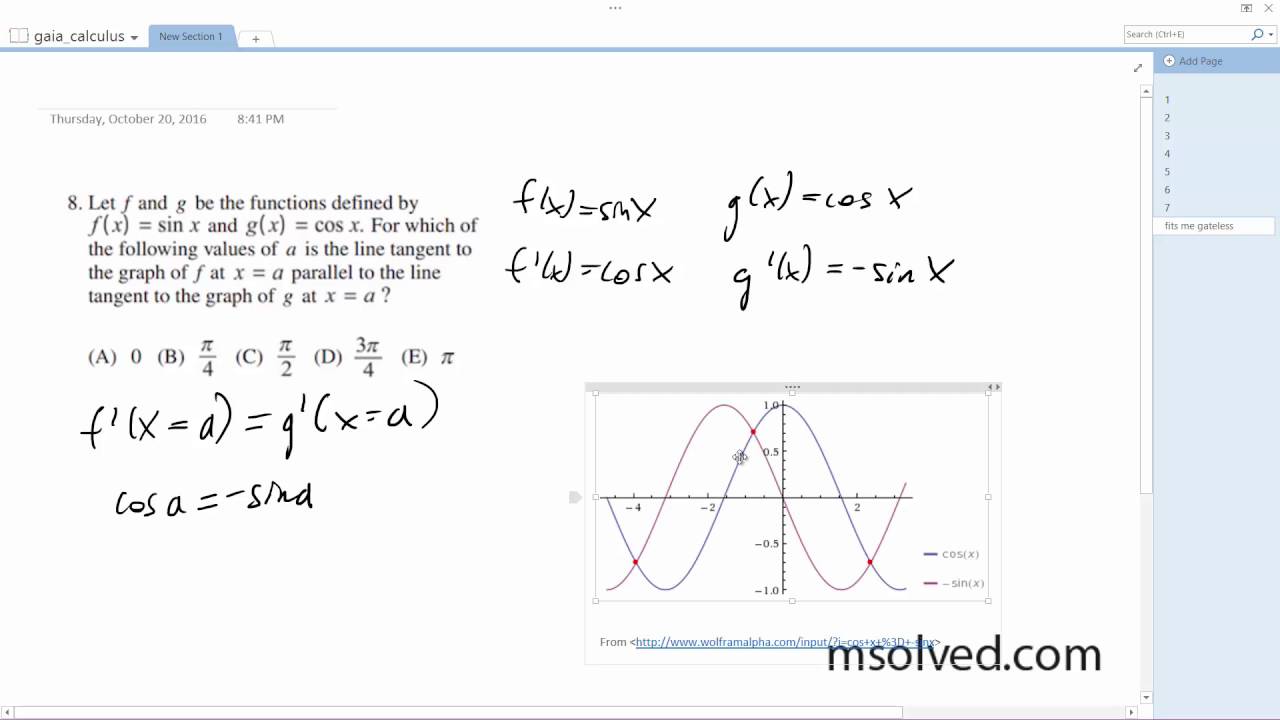



Let F And G Be The Functions Defined By F X Sin X And G X Cos X Youtube



Notes Math 414 Narcowich Cosine Sine Series




Qtiplot




Trig Functions Graphing Techniques



Are The Cosine Systems Linear Or Non Linear Quora



4 06 Graphs Of Sine And Cosine



0 件のコメント:
コメントを投稿