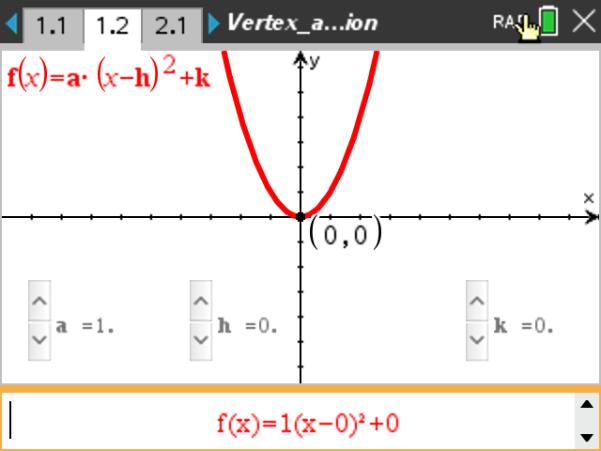
Y = a(x h) 2 Vertex Form k k vertical translation 'k' units k > 0 , the graph is translated 'k' units up k< 0 , the graph is translated 'k' units down y = x 2 4 y = x 2Correct answers 2 question Finish the steps below to write a quadratic function for the parabola shown 4 Use the vertex form, f(x) = a(x h)2 k, and substitute in the values for h and ke f(x) = a(x – 5)2 3 2 Use another point and substitute in values for x and f(x) Solve for a 5 = a(6 – 5)2 3 3 Write the function, using the values for h, k, and a The function is f(x) = Tx 12All quadratic functions include a term that contains the square of the independent variable, like x 2 There can be no higher power of x in a quadratic function Some examples are f ( x) = 2 x 2 − 3 x 1 f ( x) = ( x − 4) 2 f ( x) = − x 2 − 71 Quadratic functions have the general form

Unit 1 Graphing Quadratics Diagram Quizlet
F(x)=a(x-h)^2+k in vertex form
F(x)=a(x-h)^2+k in vertex form-The formula for the vertex form of a parabola is f(x) = a(x h) 2 k where a = vertical stretch or shrink of the parabola and (h, k) are the (x, y) coordinates of the vertex of the parabola h = the xcoordinate and k = the ycoordinate A Parabola is a Ushaped graph that is vertically symmetrical about a line that intersects the vertex ofF (x) = a(x h) 2 k, where (h, k) is the vertex of the parabola FYI Different textbooks have different interpretations of the reference " standard form " of a quadratic function Some say f ( x ) = ax 2 bx c is "standard form", while others say that f ( x ) = a ( x h ) 2 k is "standard form"



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora
Any help greatly appreciated Answer by lwsshak3 () ( Show Source ) You can put this solution on YOUR website!Multiply through the parentheses on the left Simplify on the left (converting to common denominators, if necessary), and convert to squared form on the right Move the loose numbers back over to the righthand side Convert to vertex form, as necessary Then the the vertex ( h, k) for any given quadratic y = ax 2 bx c obeys the formulaGraph of quadratic functions in vertex form g(x) = a(x h) 2 k A quadratic function in vertex form g(x) = a(x h) 2 k is the basic quadratic function f(x) = x 2 that has been transformed 1) From x 2 to (x h) 2 shift h units right if h is positive or h units left if h is negative
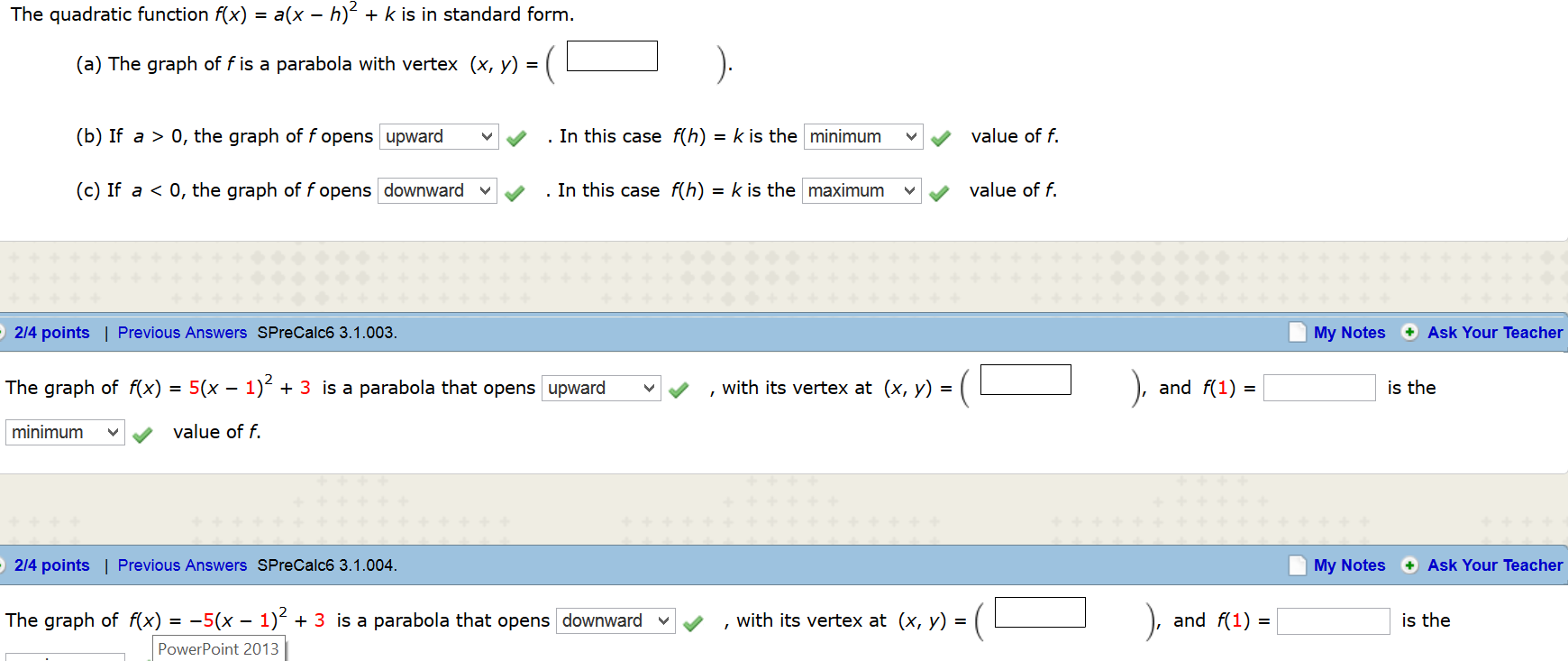
This algebra 2 and precalculus video tutorial explains how to convert a quadratic equation from standard form to vertex form with and without using the complPrecalculus (7th Edition) Edit edition Solutions for Chapter 31 Problem 2E The quadratic function f(x) = a(x−h)2 k is in standard form(a) The graph of f is a parabola with vertex (____, ____)(b) If a > 0, the graph of f opens _____ In this case f(h) = k is the _____ value of f (c) If a f opens In this case f(h) = k is the _____ value of f Isolate f(x) f(x) = (x1)^24 The equation is now in vertex form y = a(x – h)^2 k, where (h, k) is the vertex h = 1 and k = 4, so the vertex is at (1,4) Precalculus Science
The Simplest Quadratic The simplest Quadratic Equation isIn the conic section, the vertex form of a parabola is a point or place where it turns, it is also known as a turning point If the quadratic function converts to vertex form, then the vertex is (h, k) The vertex equation is y = a ( x – h) 2 kWrite the quadratic function in the form f (x)=a (xh)^2k (vertex form of equation for a parabola) Then, give the vertex of its graph f (x)=−2x^212x *** −2x^2




Unit 1 Graphing Quadratics Diagram Quizlet




Quick Review Before Hw Quiz Y A X H 2 K Form Vertex H K Axis X H Up If A 0 Down If A 0 Ex Y X 1 2 4 Y 1 X 1 2 4 A 1
LESSON 2 Graphing Quadratic Functions in Standard Form f(x)=ax^2bxc LESSON 3 Graphing Quadratic Functions in Vertex Form f(x)=a(xh)^2 k LESSON 4 Graphing Quadratic Functions in Intercept Form f(x)= a(xp)(xq) 2 Write the quadratic function in the form g ( x) = a ( x − h) 2 k Then, give the vertex of its graph g ( x) = 2 x 2 − 16 x 35 ~ I tried, but still lost ( 2 x 2 − 16 x) 35 2 ( x 2 − 4 2 − 16) 35 2 ( x 2 − 4 2 − 32 35The Graph of Quadratic Function Thank you so much for joining our Grade 9 First Quarter Math Tutorials Keep on Sharing and enjoy learning




Graphing Quadratics Vertex Form Algebra Video Khan Academy




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21
Vertex form is defined as #f(x)=a(xh)^2k# The way to find the vertex is to use #b/(2a)# (for the #h# value), and then plug that number in for #x# in the original quadratic (for the #k# value) Now that we know that, we can solve for our #h# value #b/(2a) => (3)/(2(5)) => 3/10# Now that we have our #h# value, we can plug it in for #x# in the quadraticAnswers 2 on a question Modeling, Representing and Transforming QuadraticFunctions1 f ( x ) = x 2 6 x 8 is quadratic function since its highest degree is 2 and all numerical coefficients are real numbers 2 is y =7 x 12 is not quadratic function since its highest degree 1 3 is f ( x 2) ( x 3) x 2a not quadratic function since its highest degree sana makatulong sa iyoAnswer to Write the quadratic function in the form f(x)= a(x h)^2 k Then, give the vertex of its graph f(x)= 2x^2 4x 4 By signing up,




Quadratic Functions
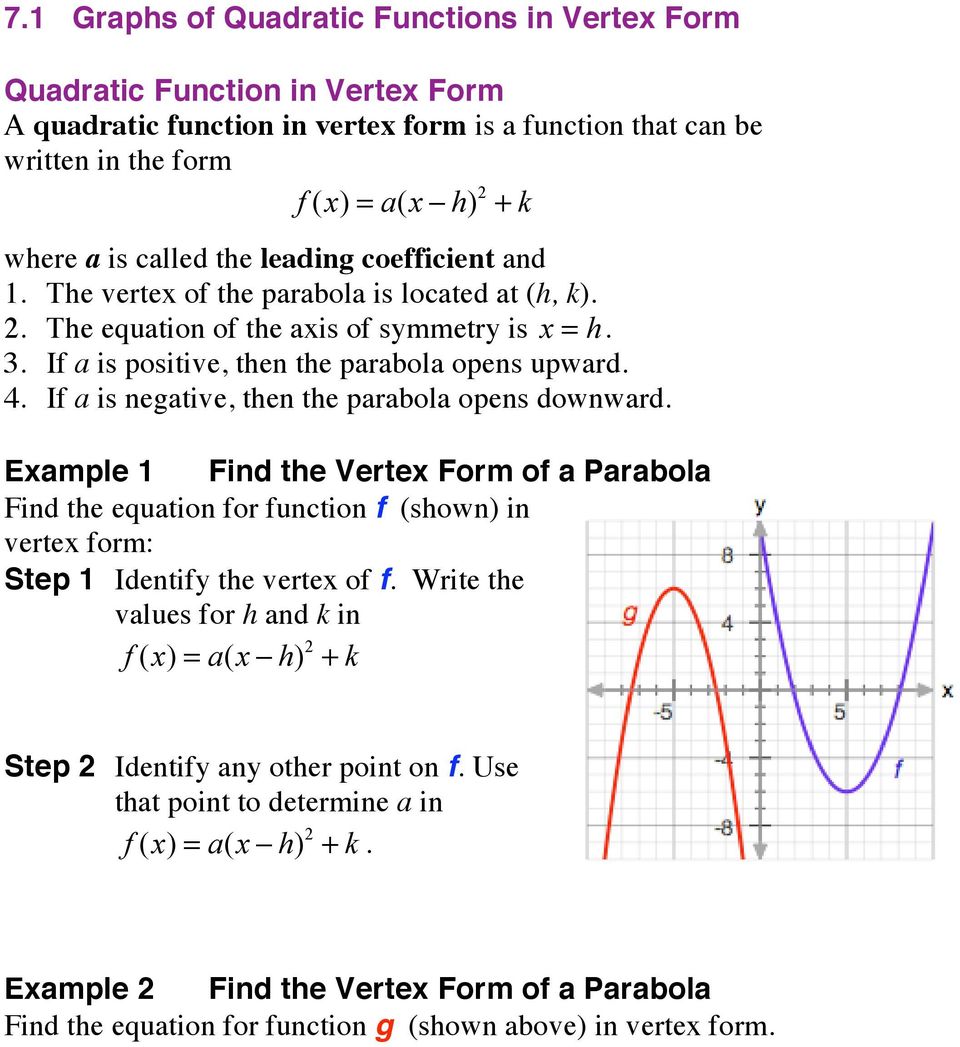



7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download
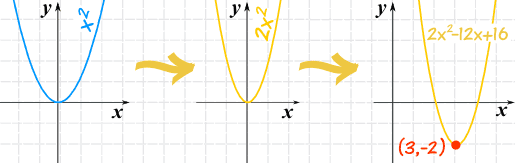
y=mxb, and y=ax^2bxc are the GENERAL form of a line, and of a parabola They are easy to use for finding y values, and more convenient if using matrices AxBy=C, and y=a (xh)^2k are the STANDARD form for a line and for a parabola The numberline intercepts are easy to identify for the line, and the vertex is easy to identify for theWe want to put it into vertex form y=a(xh) 2 k;The form of quadratic function is f(x) = a(x h)2 k, where a to and (h, k) is the vertex equation quadratic standard O vertex
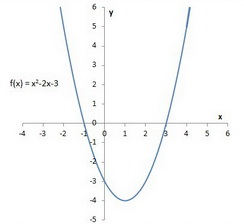



How Do I Convert The Equation F X X 2 2x 3 To Vertex Form Socratic
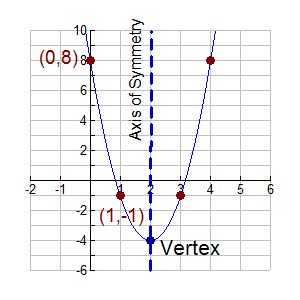



Vertex Form Of Quadratic Equation Mathbitsnotebook A1 Ccss Math
Algebra Find the Vertex Form f (x)=x^2x f (x) = x2 − x f ( x) = x 2 x Set the polynomial equal to y y to find the properties of the parabola y = x2 −x y = x 2 x Complete the square for x2 −x x 2 x Tap for more steps Use the form a x 2 b x c a x 2 b xWe can convert to vertex form by completing the square on the right hand side;Summary Our equation is in standard form to begin with y=ax 2 bxc We want to put it into vertex form y=a (xh) 2 k We can convert to vertex form by completing the square on the right hand side 36 is the value for 'c' that we found to make the right hand side a




Unit 5 Quadratic Functions Flashcards Quizlet




How To Graph A Quadratic Equation 10 Steps With Pictures
Answer to Write the quadratic function in the form f (x) = a (x h)^2 k Then, give the vertex of its graph f (x) = 2 x^2 4 x 1 ByGraphing Quadratic Equations A Quadratic Equation in Standard Form (a, b, and c can have any value, except that a can't be 0)Here is an example Graphing You can graph a Quadratic Equation using the Function Grapher, but to really understand what is going on, you can make the graph yourself Read On!The vertex form of quadratic equation is set as f(x) = a(x − h) 2 k, where in 'a' , 'h' and 'k' are all real numbers Here in, the value of is a ≠ 0 (Stitz & Zeager, 13, p198) Below are the steps to solve the given function f(x) = 3x 2 6x 2 Step 1 Translate the given function into vertex form f(x) = a(x − h) 2 k f(x) = 3x 2 6x 2



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora



1
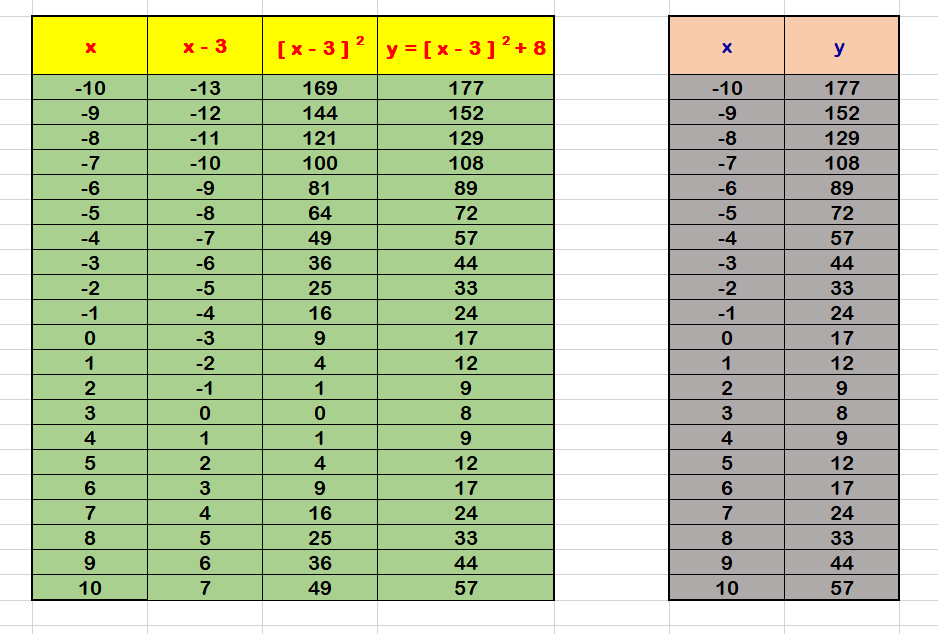
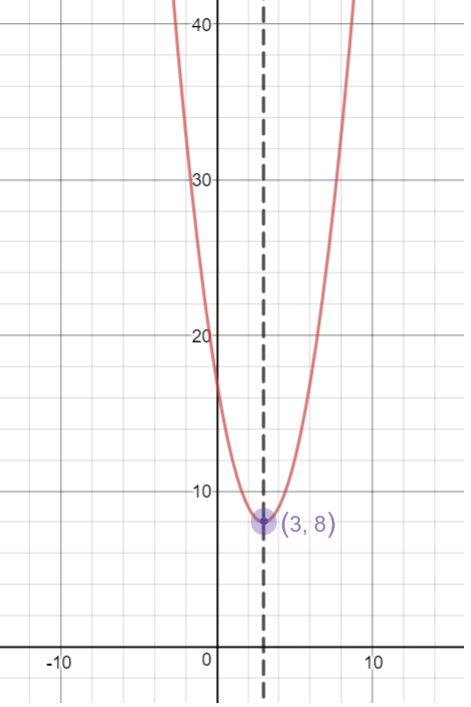
The vertex of a quadratic equation in vertex form is (h,k), so our vertex is (3C) f(x) = 2(x 3) 2 = 2(x 3)) 2 0 a = 2 , h = 3 and k = 0 The vertex is at (3,0) and it is a minimum point since a is positive Interactive Tutorial Use the html 5 (better viewed using chrome, firefox, IE 9 or above) applet below to explore the graph of a quadratic function in vertex form f(x)=a (xh) 2 k where the coefficients a, h() = is called the vertex form, where h and k are the x and y coordinates of the vertex, respectively The coefficient a is the same value in all three forms To convert the standard form to factored form, one needs only the quadratic formula to determine the two roots r 1 and r 2



The Quadratic Function F X A X H 2 K Is In Chegg Com



Solution Write The Given Expression In The Form F X A X H 2 K Identify The Vertex F X 6 5x 10x 2
Solution for Write the function in f(x) = a(x − h)2 k form Determine the vertex and the axis of symmetry of the graph of the function f(x) = 9x2 54xAnswer choices f (x) = 2a (x h) 2 k f (x) = a (x h) 2 k f (x) = (x h) 2 k f (x) = a (x h) kTranscribed image text Write the given expression in the form f(x)= a(xh)2 k Identify the vertex f(x) = 3x2 12x2 f(x)=17 (Simplify your answer Use integers or fractions for any numbers in the expression) Enter your answer in the answer box and then click Check Answer Clear All




Vertex Form Of A Quadratic Function Y A X H 2 K The Vertex Form Of A Quadratic Function Is Given By F X A X H 2
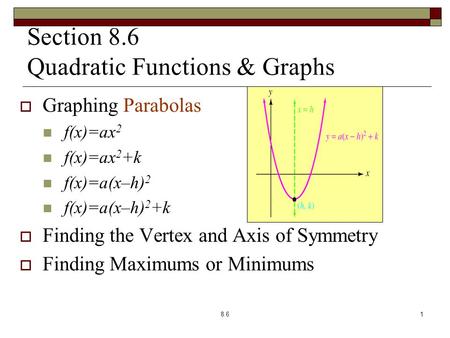



Transformations Review Vertex Form Y A X H 2 K The Vertex Form Of A Quadratic Equation Allows You To Immediately Identify The Vertex Of A Parabola Ppt Download
Example 523 Complete the square to place f(x) = x2 6x 2 in vertex form and sketch its graph Solution First, take half of the coefficient of x and square; The standard form of a quadratic function presents the function in the form \f(x)=a(x−h)^2k\ where \((h, k)\) is the vertex Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic functionFind the Vertex f(x)=x^26x5 Rewrite the equation in term of and Rewrite the equation in vertex form Tap for more steps Complete the square for Substitute the values of , , and into the vertex form Set equal to the new right side Use the vertex form, ,




Finding Vertex Form Of A Quadratic Equation Learnmath
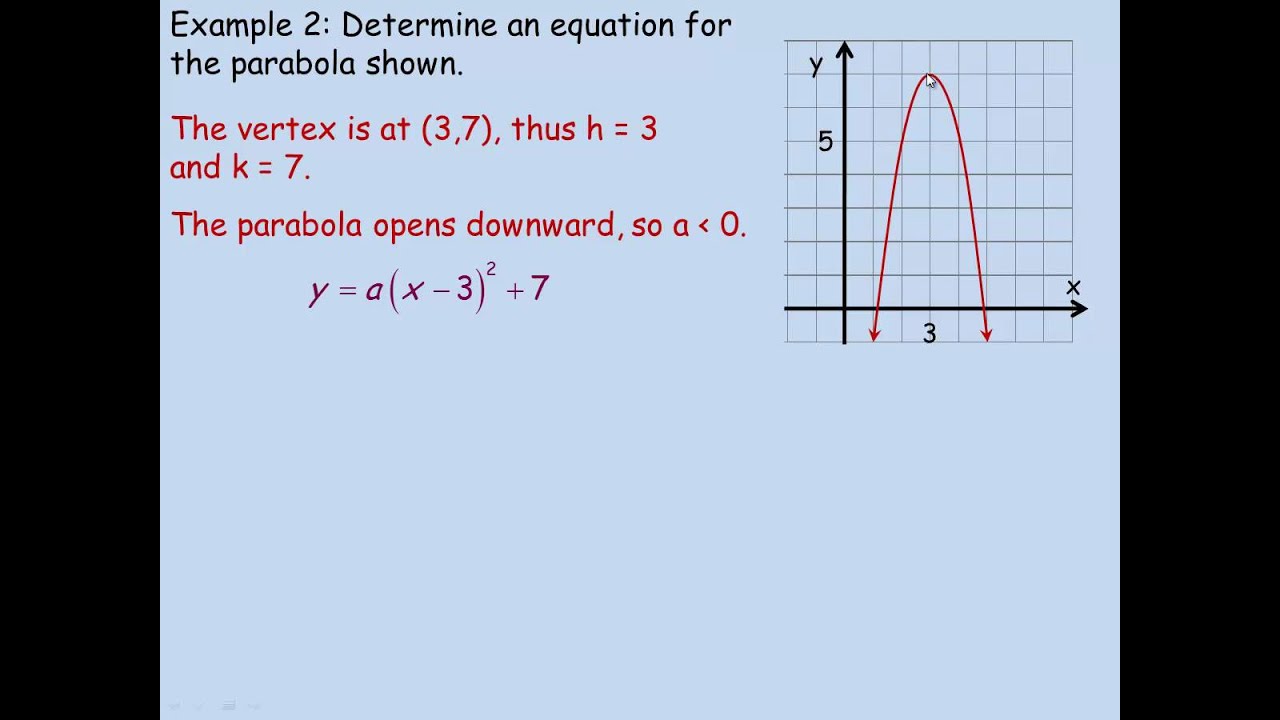



Graphing Y A X H K Youtube
V(4,2) In the vertex form, the h value is the x and the k value is the y So if the vertex (4,2) is also (h,k) You can just simply replace the h and k in (xh)^2k Given that the vertex (h, k) is (5, 2), you know the vertex form will look like f (x) = a (x 5)² 2 for some value of "a" that makes f (4) = 3 That value of "a" can be found by substituting the given values in the above equation for f (x) and solving for "a" 3 = a (4 5)² 2Algebra > Quadratic Equations and Parabolas > SOLUTION Write the quadratic function in the form f(x)=a(xh)^2k Then, give the vertex of its graph f(x)=2x^2x52 Log On Quadratics solvers Quadratics Practice!
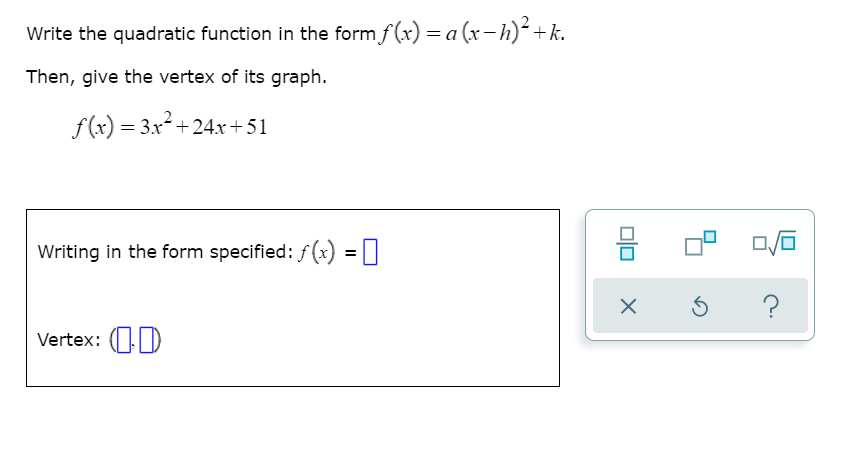



Answered Write The Quadratic Function In The Bartleby




Quadratic Function Pdf Quadratic Equation Equations
Similarly, Consider the graph of the parabola y = ax2 Its vertex is clearly at (0,0) Now, if you replace x with x−h in any equation, its graph gets shifted to the right by a distance of h Similarly, 0=a (xh)^2k 0 = a(x −h)2 k https//wwwtigeralgebracom/drill/0=a (xh)~2_k/Vertex Form f(x) = a(x h)2 k %3D Directions Transformations from the parent function y = x² are described below Write an equation to represent the function A translated 2 units right B translated 5 units upIe, (1 / 2)(6)2 = 9 On the right side of the equation, add and subtract this amount so as to not change the equation f(x) = x2 6x 9 − 9 2




6 6 Analyzing Graphs Of Quadratic Functions




Standard 9 Write A Quadratic Function In Vertex Form Ppt Video Online Download
Avertex form f(x) = 10(x 4)2 5 standard form f(x) = −10x2 40x 165 bvertex form f(x) = −6(x − 4)2 3 standard form f(x) = −6x2 7x − 24 cvertex form f(x) = −10(x − 2)2 3 standard form f(x) = −10x2 40x − 37 dvertex form f(x) = −3(x − 2)2 4 standard form f(xAdding 18 to both sides gives us a perfect square trinomial on the right; Find the vertex equation form, f(x)=a(xh)^2k, for a parabola that passes through the point(6,9)and has(5,8)as it's vertex what is the standard form of the equation Categories Uncategorized Leave a Reply Cancel reply




Ex Write Ax 2 Bx C In The Form A X H 2 K Negative A Youtube



Y A X H 2 K Transformations
Graphing f (x) = a(x − h)2 k The vertex form of a quadratic function is f (x) = a(x − h)2 k, where a ≠ 0 The graph of f (x) = a(x − h)2 k is a translation h units horizontally and k units vertically of the graph of f (x) = ax2 The vertex of the graph of f (x) = a(x − h)2 k is (h, k), and the axis of symmetry is x = h h f(xSo this simplifies be negative two times X minus three squared is equal to 11 minus 18 18 is 7 So now we write the equation of vertex form So F Of X Or not If a bex this is Q Of X Q Of X is equal to negative two times the quantity x minus three squared to move the seven back over and it becomes plus seven What is the vertex form, f(x) = a(x − h)2 k, for a parabola that passes through the point (1, −7) and has (2, 3) as its vertex what is the standard form of the equation?




Quadratic Function Wikipedia



Vertex And Intercepts
Graph By Transformations F X A X H 2 K Youtube For more information and source, see on this link https//wwwyoutubecom/watch?v=fid6PLHoouQOur equation is in standard form to begin with y=ax 2 bxc;180 seconds Report an issue Q What is the vertex form of a quadratic function?



Illustrative Mathematics



Vertex And Intercepts



Illustrative Mathematics




Graphing A Parabola In The Form Y X H 2 K Youtube




7 1 Graphs Of Quadratic Functions In Vertex Form Quadratic Flip Ebook Pages 1 39 Anyflip Anyflip




Standard Form To Vertex Form Without Completing The Square Method Algebra 2 Youtube




Quadratic Equations Parabolas Flashcards Quizlet




I Need To Write The Given Function In The Form Of Chegg Com



Illustrative Mathematics




7 1 Graphs Of Quadratic Functions In Vertex Form Quadratic Flip Ebook Pages 1 39 Anyflip Anyflip




Quadratic Functions




Algebra Ii 9 5a Graphs Of F X A X H K Guidelines For Graphing Quadratic Functions Youtube




Graphing Parabolas




6 6 Analyzing Graphs Of Quadratic Functions




1 A Write The Quadratic Function F X 3x2 12x Chegg Com




Vertex Form Equation Functions Video Lesson Transcript Study Com
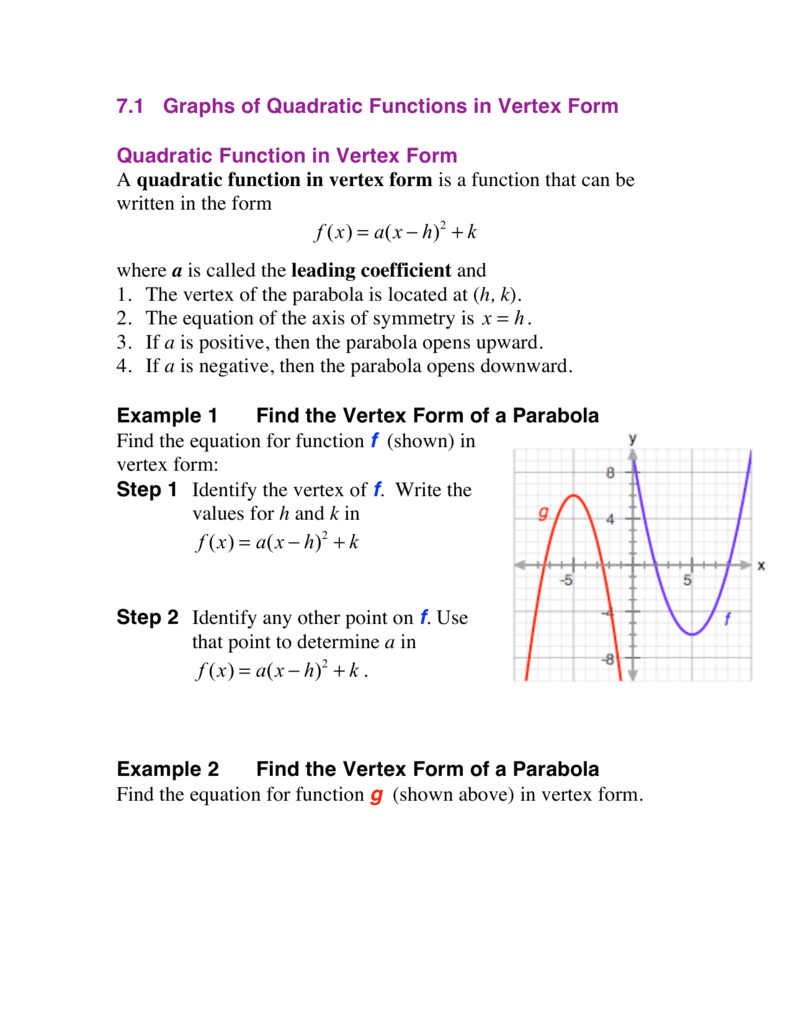



F X A X H 2 K F X A X H 2 K F X A X H 2 K
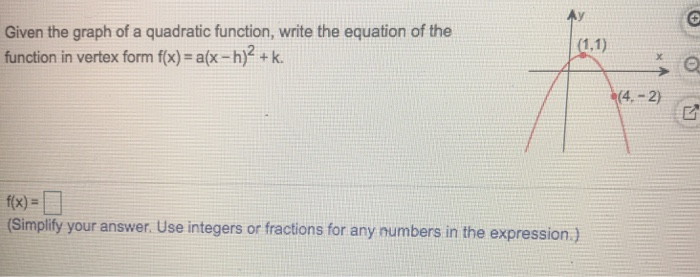



Given The Graph Of A Quadratic Function Write The Chegg Com




Vertex Intercept And Standard Form Read Algebra Ck 12 Foundation



Staffweb Psdschools Org Eharding Alg1v Bigideasch 8 A1v8 4notesgraphingf A Xh K Pdf
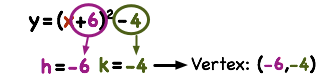



How Do You Convert A Quadratic From Standard Form To Vertex Form By Completing The Square Printable Summary Virtual Nerd



Solved Use The Graph Of A Quadratic Function F To Write Its Formula As F X A X H 2 K F X Course Hero




Ppt Quadratics Of The Form Y A X H 2 K Powerpoint Presentation Id
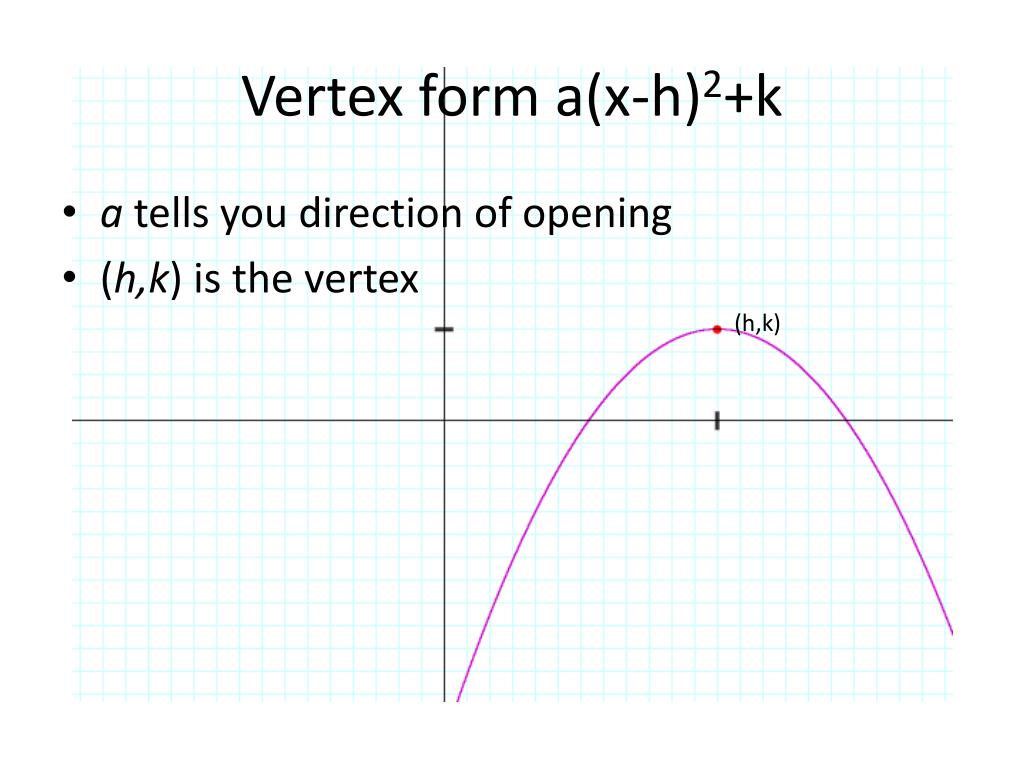



Ppt Vertex Form Powerpoint Presentation Free Download Id




Rewrite The Following Quadratic Functions In Chegg Com
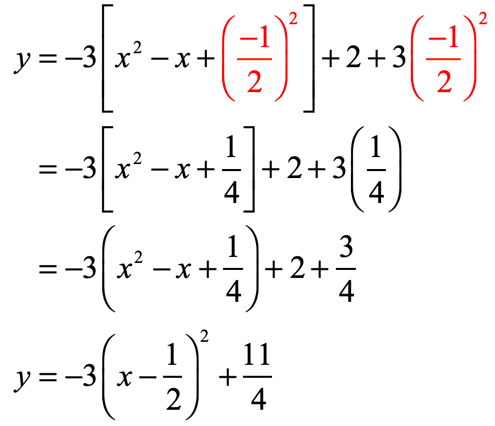



Completing The Square Step By Step Chilimath



When You Use The Vertex Form Y A X H 2 K What Information Do You Get From A Vertex Form Quora



Vertex Form Of A Quadratic Equation Algebra Socratic




Converting A Quadratic Function From Standard Form To Vertex Form Completing The Square Youtube




The Vertex Form Of A Quadratic Function Is F X A X H 2 K What Is The Vertex Of Each Function Brainly Com




Algebra 2 Section 2 1 Part 2 29 Minutes Yankton High School




Quadratic Word Problems Vertex Form Video Khan Academy




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21




1 3 Maximum Or Minimum Of A Quadratic Function Investigate A Pdf Free Download



1




Quadratic Functions



Solution Write The Given Expression In The Form F X A X H 2 K Identify The Vertex F X 1 3x 2 X 1 If You Could Please Show Me Step By Step Thanks




Transform The Following Quadratic Function Into The Vertex Form F X A X H 2 K And Identify The Brainly Ph



Vertex Form Of A Quadratic Equation Algebra Socratic



Graphing Quadratic Equations




3 Ways To Find The Maximum Or Minimum Value Of A Quadratic Function Easily




The Vertex Form Of A Quadratic Function Is F X A X H 2 K What Is The Vertex Of Each Function Brainly Com




Finding The Vertex Of A Parabola In Standard Form Video Khan Academy




Functions Flashcards Quizlet




What Is Vertex Form Example Get Education




Quadratic Functions Ppt Download




Write The Quadratic Function In The Form F X Chegg Com




The Vertex Of The Parabola Is At H K Ppt Video Online Download



Http Www Math Wsu Edu Faculty Dzhang 1fall14 1lecturenotes Fall14 Wed9 10 Pdf



Algebra 2 Vertex And Factored Form Of Quadratic Functions Algebra Ii Ti Math Nspired




Quadratic Functions Equations Dev Serum




6 6 Analyzing Graphs Of Quadratic Functions




Write The Quadratic Function In The Form G X Chegg Com




Quadratic Functions



Sections 6 And 8 Quadratics Part 2 And Polynomial Functions



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola




Section 5 3 Transforming Parabolas Standard Form Vs Vertex Form Standard Form Is Y Ax 2 Bx C Vertex Form Is Y A X H 2 K Ppt Download



Graphing Quadratic Functions Course Hero



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola




How To Graph A Quadratic Equation 10 Steps With Pictures
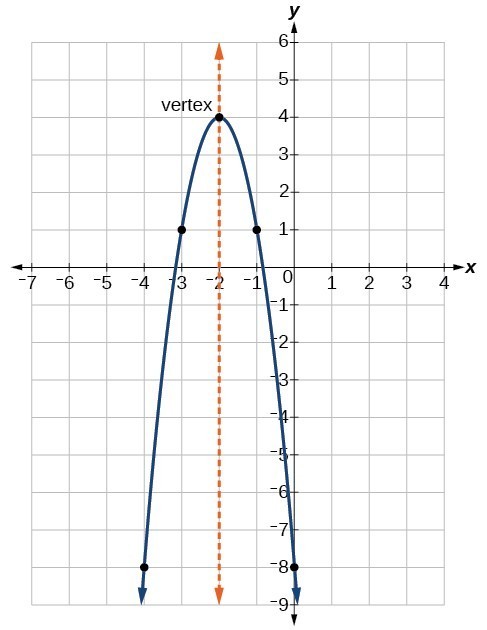



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra
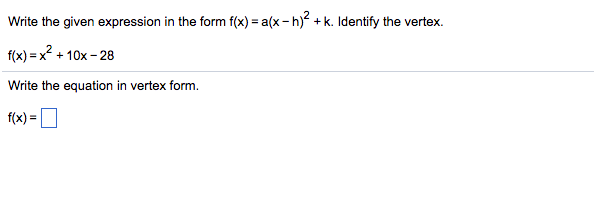



Write The Given Expression In The Form F X A X Chegg Com




Y A X H 2 K Algebra 2 Notes 4 1 4 2 Pg 236 Pg 245 Pg Ppt Video Online Download




Calgebra A1 8 4 Graphing F X A X H 2 K Youtube



Graphing Quadratic Functions
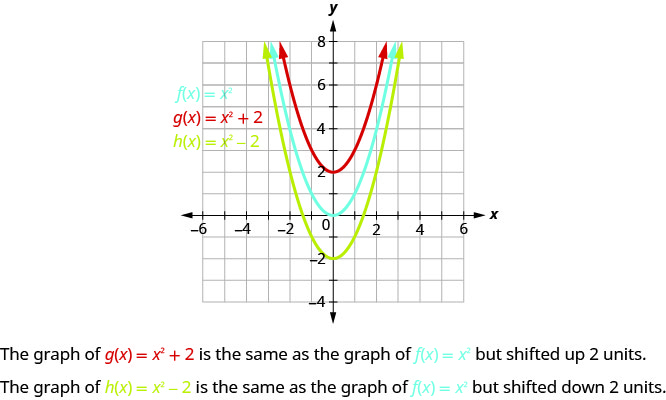



6 7 Graph Quadratic Functions Using Transformations Mathematics Libretexts



Sections 6 And 8 Quadratics Part 2 And Polynomial Functions



Graphing Quadratic Functions In Vertex Or Intercept Form
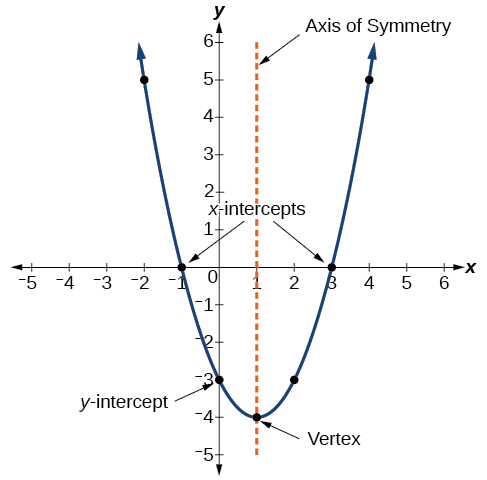



5 2 Quadratic Functions Mathematics Libretexts
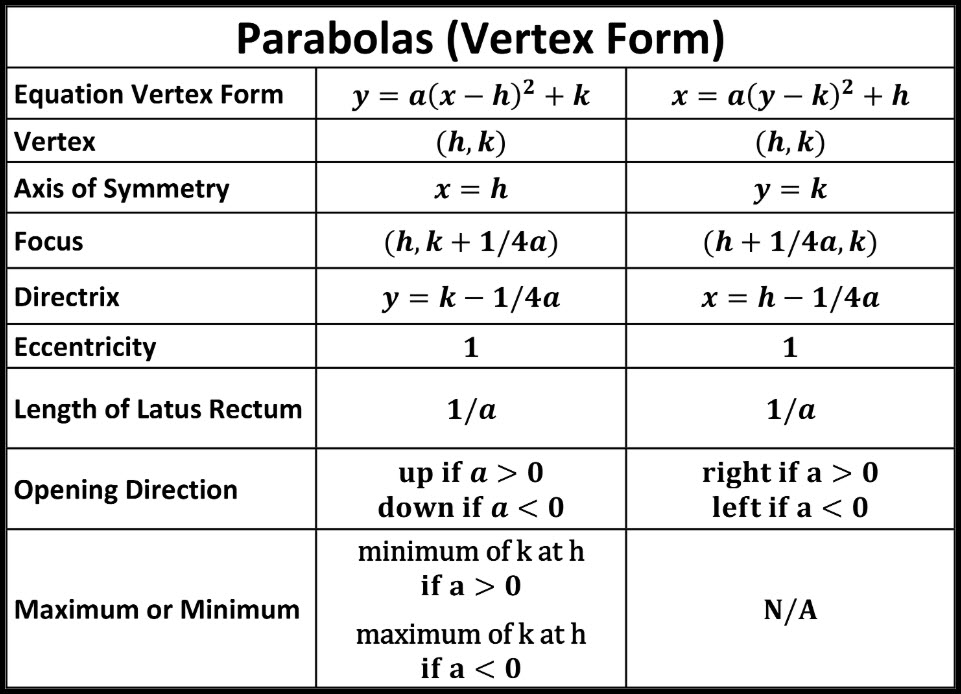



Parabolas Andymath Com



Quadratic Functions



Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 p2 unit 2 2 note packet lg 1019 complete lt 8 to end Pdf



Q Tbn And9gcsii Oy2yypz9rkmjcuovykbdun8vt6fypixxp7i8sk9 6iuq4 Usqp Cau
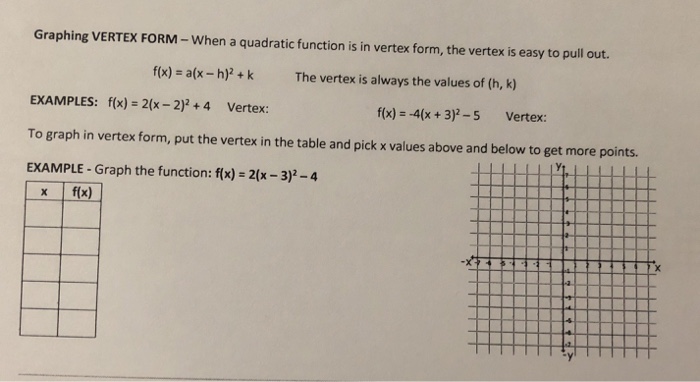



Graphing Vertex Form When A Quadratic Function Is In Chegg Com




Changing A Quadratic Function Into Vertex Form Youtube
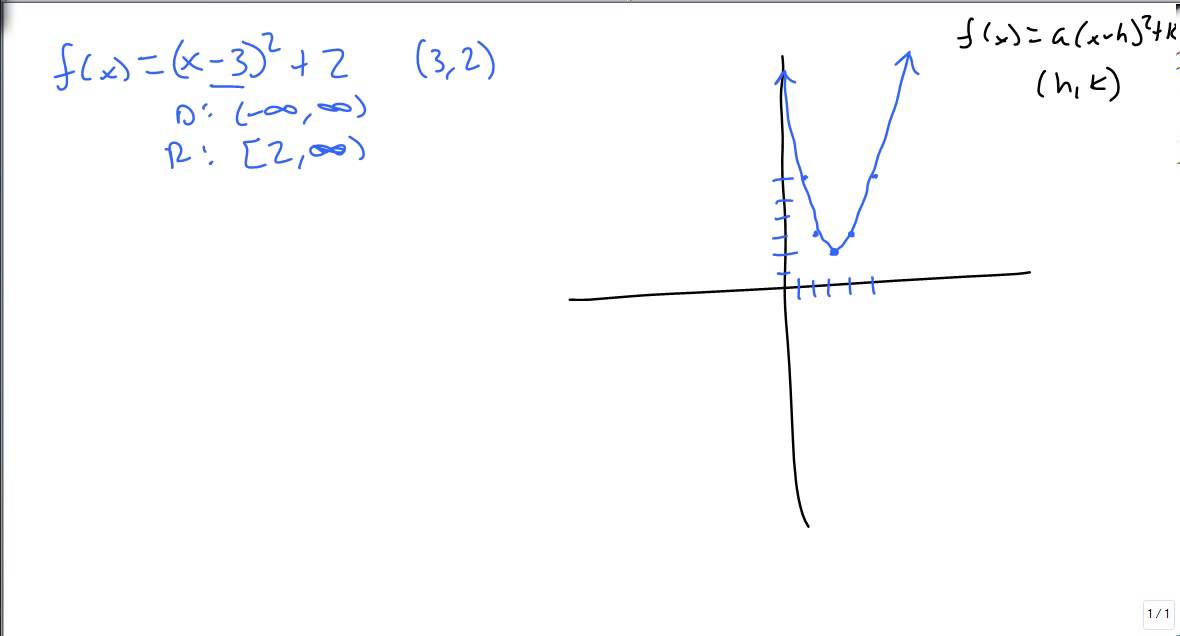



Graph By Transformations F X A X H 2 K Youtube



Solution Write The Quadratic Function In The Form F X A X H 2 K Find The Vertex And Graph The Function A F X X 2 6x B F X X 2 4x 1 C F X 3x 2 10x 2
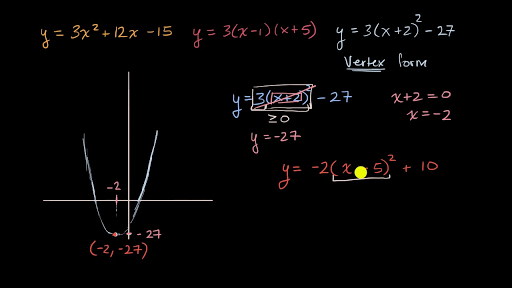



Vertex Form Introduction Video Khan Academy



0 件のコメント:
コメントを投稿